
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
在平面直角坐标系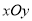 中,直线
中,直线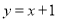 与双曲线
与双曲线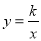 的一个交点为P(m,2).
的一个交点为P(m,2).
(1)求k的值;
(2)M(2,a),N(n,b)是双曲线上的两点,直接写出当a > b时,n的取值范围.
(1);(2)或 【解析】试题分析:(1)将点P代入y=x+1,求出m的值,然后再将点P代入反比例解析式即可得; (2)根据反比例函数的性质分情况讨论即可得. 试题解析:(1)一次函数的图象经过点, , 点P的坐标为(1,2), ∵反比例函数的图象经过点P(1,2), ; (2)当x=2时, =1,所以M(2,1),a=1, 若点N(n,b)在第一象...查看答案和解析>>
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
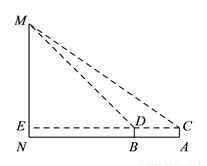
在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)

查看答案和解析>>
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线. 如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,求水流的落地点C到水枪底部B的距离.
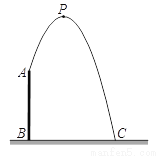
查看答案和解析>>
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
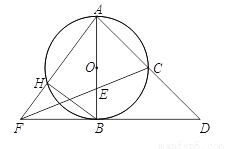
如图, 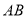 是⊙O的直径,点
是⊙O的直径,点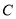 是
是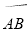 的中点,连接
的中点,连接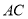 并延长至点
并延长至点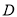 ,使
,使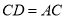 ,点
,点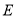 是
是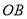 上一点,且
上一点,且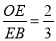 ,
, 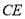 的延长线交
的延长线交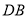 的延长线于点
的延长线于点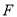 ,
, 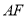 交⊙O于点
交⊙O于点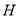 ,连接
,连接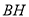 .
.
(1)求证: 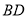 是⊙O的切线;
是⊙O的切线;
(2)当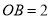 时,求
时,求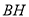 的长.
的长.
查看答案和解析>>
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
如图,点E是矩形ABCD边AB上一动点(不与点B重合),过点E作EF⊥DE交BC于点F,连接DF.已知AB = 4cm,AD = 2cm,设A,E两点间的距离为xcm,△DEF面积为ycm2.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
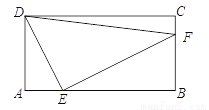
下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y/cm2 | 4.0 | 3.7 | 3.9 | 3.8 | 3.3 | 2.0 | … |
(说明:补全表格时相关数值保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(4)结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为 cm.
(1);(2)3.8,4.0;(3)画图见解析;(4)0或2. 【解析】试题分析:(1)根据点E是边AB上一动点(不与点B重合)即可得; (2)由题意可得△ADE∽△BEF,由相似三角形对应边成比例可以得到用x表示的BF,由y=S矩形ABCD -S△ADE-S△BEF-S△DCF 根据表格中的数据进行计算即可得; (3)根据表格中的数据进行描点,然后用平滑的曲线连接即可得; ...查看答案和解析>>
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
在平面直角坐标系xOy中,抛物线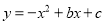 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(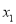 ,
, 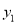 ),B(
),B(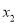 ,
, 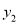 ),其中
),其中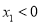 ,
, 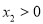 ,与y轴交于点C,求BC
,与y轴交于点C,求BC AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
(1);(2)BC-AC=2;(3)点Q的坐标为()或(). 【解析】试题分析:(1)由抛物线经过点(2,3),对称轴为直线x =1,利用待定系数法即可得; (2)如图,设l与对称轴交于点M,根据抛物线的对称性,可知AM=BM, AM=AC+CM,BC=BM+CM,推导即可得; (3)由OP=OQ可知P、Q两点关于x轴对称,求出平移后的解析式,表示出P、Q的坐标,根据关于x轴对称...查看答案和解析>>
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.
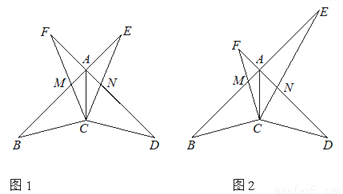
查看答案和解析>>
科目: 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:如果⊙C的半径为r,⊙C外一点P到⊙C的切线长小于或等于2r,那么点P叫做⊙C的“离心点”.
(1)当⊙O的半径为1时,
①在点P1(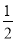 ,
, 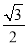 ),P2(0,-2),P3(
),P2(0,-2),P3(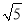 ,0)中,⊙O的“离心点”是 ;
,0)中,⊙O的“离心点”是 ;
②点P(m,n)在直线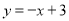 上,且点P是⊙O的“离心点”,求点P横坐标m的取值范围;
上,且点P是⊙O的“离心点”,求点P横坐标m的取值范围;
(2)⊙C的圆心C在y轴上,半径为2,直线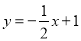 与x轴、y轴分别交于点A,B. 如果线段AB上的所有点都是⊙C的“离心点”,请直接写出圆心C纵坐标的取值范围.
与x轴、y轴分别交于点A,B. 如果线段AB上的所有点都是⊙C的“离心点”,请直接写出圆心C纵坐标的取值范围.
查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
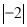 的相反数是( )
的相反数是( )
A. 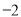 B.
B. 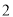 C.
C. 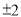 D.
D. 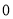
查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
近年来,国家重视精准扶贫,收效显著,据统计到目前为止约有65 000 000人脱贫.则65 000 000用科学记数法表示正确的是( )
A. 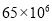 B.
B. 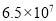 C.
C. 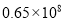 D.
D. 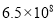
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com