练习册

  • 练习册
  • 试题
    相关习题
     0  320952  320960  320966  320970  320976  320978  320982  320988  320990  320996  321002  321006  321008  321012  321018  321020  321026  321030  321032  321036  321038  321042  321044  321046  321047  321048  321050  321051  321052  321054  321056  321060  321062  321066  321068  321072  321078  321080  321086  321090  321092  321096  321102  321108  321110  321116  321120  321122  321128  321132  321138  321146  366461 

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

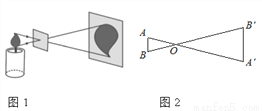
    如图1，物理课上学习过利用小孔成像说明光的直线传播.现将图1抽象为图2，其中线段AB为蜡烛的火焰，线段A＇B＇为其倒立的像. 如果蜡烛火焰AB的高度为2cm，倒立的像A＇B＇的高度为5cm，点O到AB的距离为4cm，那么点O到A＇B＇的距离为__________ cm.

    10 【解析】过点O作OC⊥AB于点C，延长CO交A＇B＇ 于点D， ∵AB// A＇B＇，∴CD⊥A＇B＇，△AOB∽△A＇OB＇， ∴ ， 即 ， ∴OD=10cm， 故答案为：10.

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

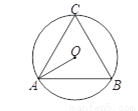
    如图，等边三角形ABC的外接圆⊙O的半径OA的长为2，则其内切圆半径的长为__________.

    1 【解析】过点O作OD⊥AB于点D， ∵△ABC是等边三角形， ∴∠OAD=30°， ∵∠ADO=90°，∴OD=AO==1， 即其内切圆半径的长为1， 故答案为：1.

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

    已知函数的图象经过点（2，1），且与x轴没有交点，写出一个满足题意的函数的表达式__________.

    或等，答案不唯一 【解析】一次函数与x轴有交点，反比例函数与x轴无交点，二次函数在满足b2-4ac<0的条件时与x轴无交点，因此满足题意的函数可以是反比例函数或是满足条件的二次函数， 函数的图象经过点（2，1），且与x轴没有交点的函数的表达式可以是： 或等，答案不唯一， 故答案为： 或（答案不唯一）.

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

    在平面直角坐标系中，过三点A（0，0），B（2，2），C（4，0）的圆的圆心坐标为__________.

    （2，0） 【解析】过点B作BD⊥AC， ∵A（0，0），B（2，2），∴BD=AD=2，∴∠ABD=∠BAD=45°， 又∵C（4，0），∴CD=AD=2=BD，∴∠DCB=∠DBC=45°， ∴∠ABC=90°， ∴点A、B、C三点在以点D为圆心，AD长为半径的圆上， 所以圆心的坐标为（2，0）， 故答案为：（2，0）.

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

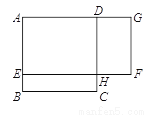
    在北京市治理违建的过程中，某小区拆除了自建房，改建绿地. 如图，自建房占地是边长为8m的正方形ABCD，改建的绿地是矩形AEFG，其中点E在AB上，点G在AD的延长线上，且DG = 2BE. 如果设BE的长为x（单位：m），绿地AEFG的面积为y（单位：m2），那么y与x的函数的表达式为__________________；当BE =______m时，绿地AEFG的面积最大.

    2 【解析】由题意可知：AE=AB-BE=8-x，DG=2BE=2x，所以AG=AD+DG=8+2x， ∴y=AE·AG=（8-x）(8+2x)=-2x2+8x+64(0

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

    下面是“过圆外一点作圆的切线”的尺规作图过程.

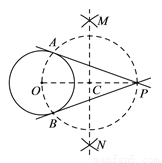
    请回答以下问题：

    （1）连接OA，OB，可证∠OAP =∠OBP = 90°，理由是______________________；

    （2）直线PA，PB是⊙O的切线，依据是__________________________________．

    直径所对的圆周角是直角 经过半径的外端，并且垂直于这条半径的直线是圆的切线 【解析】（1）根据作图可知PO是⊙C的直径，根据直径所对的圆周角是直角，可得证∠OAP =∠OBP = 90°， 故答案为：直径所对的圆周角是直角； （2）∵∠OAP=∠OBP=90°，OA、OB是⊙O的直径，∴PA、PA是⊙O的切线（经过半径的外端，并且垂直于这条半径的直线是圆的切线）， 故答案为...

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：解答题

    计算： .

    【解析】试题分析：把特殊角的三角函数值代入进行计算即可. 试题解析： ===.

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：解答题

    如图，△ABC中，DE∥BC，如果AD = 2，DB = 3，AE = 4，求AC的长.

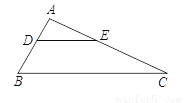
    AC＝10． 【解析】试题分析：根据平行线分线段成比例定理求得EC的长即可得. 试题解析：∵DE∥BC， ∴ 即． ∴EC＝6． ∴AC＝AE + EC＝10．

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：解答题

    已知二次函数y = x2 - 4x + 3．

    （1）用配方法将y = x2 - 4x + 3化成y = a(x - h)2 + k的形式；

    （2）在平面直角坐标系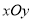中画出该函数的图象；

    （3）当0≤x≤3时，y的取值范围是 .

    （1）y ；（2）画图见解析；（3） 【解析】试题分析：（1）根据配方法的步骤进行整理即可得； （2）根据解析式确定出对称轴、与x轴、y轴的交点坐标，然后进行画图即可； （3）观察图象即可得. 试题解析：（1） ； （2）由y = x2 - 4x + 3，可知与x轴的交点坐标为：（1，0）、（3，0）， 与y轴的交点坐标为（0，3）， 由（1）可知对称轴为...

    查看答案和解析>>

    科目： 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：解答题

    在我国古代数学著作《九章算术》中记载了这样一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现代语言表述为：如图，AB为⊙O的直径，弦CD⊥AB于点E，AE = 1寸，CD = 10寸，求直径AB的长．请你解答这个问题.

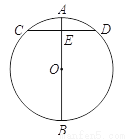
    直径AB的长26寸． 【解析】试题分析：连接OC．先根据垂径定理求出CE=CD，设半径为r，则OE =r-1，在Rt中， 根据勾股定理求得r的长，即可求解． 试题解析：连接OC， ∵AB为⊙O的直径，弦CD⊥AB于点E，且CD=10， ∴∠BEC＝90°，， 设OC=r，则OA=r，∴OE= ， 在Rt中， ∵， ∴，∴， ∴AB = 2...

    查看答案和解析>>

    同步练习册答案