
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
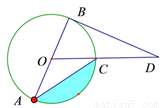
如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4.
(1) 求∠BAC的大小;
(2) 求图中阴影部分的面积.
查看答案和解析>>
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
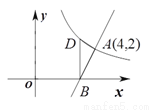
如图,直线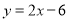 与反比例函数
与反比例函数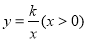 的图象交于点
的图象交于点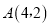 ,与
,与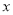 轴交于点
轴交于点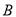 .
.
(1)求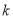 的值及点
的值及点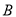 的坐标;
的坐标;
(2)过点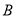 作
作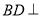
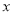 轴交反比例函数的图象于点
轴交反比例函数的图象于点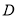 ,求点D的坐标和
,求点D的坐标和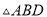 的面积;
的面积;
(3)观察图象,写出当x>0时不等式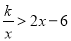 的解集.
的解集.
查看答案和解析>>
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在正方形网格中, 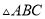 的三个顶点都在格点上,点
的三个顶点都在格点上,点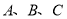 的坐标分别为
的坐标分别为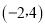 、
、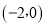 、
、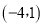 ,试解答下列问题:
,试解答下列问题:
(1)画出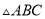 关于原点
关于原点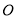 对称的
对称的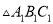 ;
;
(2)平移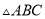 ,使点
,使点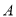 移到点
移到点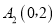 ,画出平移后的
,画出平移后的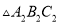 并写出点
并写出点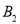 、
、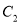 的坐标;
的坐标;
(3)在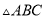 、
、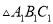 、
、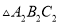 中,
中, 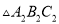 与哪个图形成中心对称?试写出其对称中心的坐标.
与哪个图形成中心对称?试写出其对称中心的坐标.

查看答案和解析>>
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
(1)0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0);(2). 【解析】 试题分析:(1)根据题意可得,x有三种等可能取值,即0,1,2;在每个取值下面,y都有三种等可能取值即:-1,-2,0,所以M点坐标共有9种等可能情况,分别是(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,...查看答案和解析>>
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
“国庆”期间,某电影院装修后重新开业,试营业期间统计发现,影院每天售出的电影票张数y(张)与电影票售价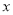 (元/张)之间满足一次函数关系:
(元/张)之间满足一次函数关系: 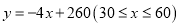 ,
, 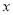 是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入
是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入 运营成本).
运营成本).
(1)试求w与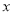 之间的函数关系式;
之间的函数关系式;
(2)影院将电影票售价定为多少时,每天获利最大?最大利润是多少元?
(1);(2)32元,最大利润是2624元. 【解析】试题分析:(1)根据“利润=票房收入-运营成本”可得函数解析式; (2)将函数解析式配方成顶点式,由30≤x≤60,且x是整数结合二次函数的性质求解可得. 试题解析: 解:(1)由题意: , 得w与之间的函数关系式为: . (2), . 是整数, , 当或33时,w取得最大值,最大值为...查看答案和解析>>
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
关于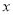 的方程
的方程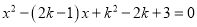 有两个不相等的实数根.
有两个不相等的实数根.
(1)求实数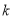 的取值范围;
的取值范围;
(2)设方程的两个实数根分别为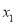
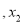 ,是否存在实数k,使得
,是否存在实数k,使得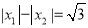 ?若存在,试求出
?若存在,试求出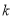 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且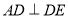 于D,与⊙O交于点F.
于D,与⊙O交于点F.
(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线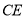 的长.
的长.

查看答案和解析>>
科目: 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
已知抛物线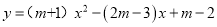 的图象与
的图象与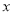 轴有两个公共点.
轴有两个公共点.
(1)求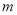 的取值范围,写出当
的取值范围,写出当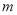 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为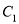 ,
,
①求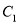 的顶点
的顶点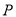 的坐标;
的坐标;
②若当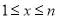 时,
时, 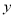 的取值范围是
的取值范围是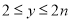 ,求
,求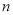 的值;
的值;
(3)将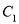 平移得到抛物线
平移得到抛物线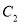 ,使
,使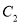 的顶点
的顶点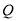 落在以原点为圆心半径为
落在以原点为圆心半径为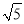 的圆上,求点
的圆上,求点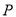 与
与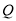 两点间的距离最大时
两点间的距离最大时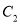 的解析式,怎样平移
的解析式,怎样平移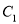 可以得到所求抛物线?
可以得到所求抛物线?

查看答案和解析>>
科目: 来源:福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
36的平方根是( )
A. 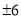 B.
B. 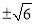 C.
C. 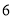 D.
D. 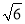
查看答案和解析>>
科目: 来源:福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列计算正确的是( )
A. 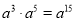 B.
B. 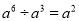 C.
C. 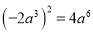 D.
D. 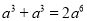
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com