
科目: 来源:安徽省2017-2018学年七年级上学期期末统一质量检测数学试卷 题型:解答题
有这样一道题:“先化简,再求值: 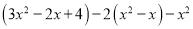 ,其中
,其中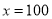 ”甲同学做题时把
”甲同学做题时把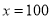 错抄成了
错抄成了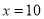 ,乙同学没抄错,但他们做出来的结果却一样,你能说明这是为什么吗?并求出这个结果.
,乙同学没抄错,但他们做出来的结果却一样,你能说明这是为什么吗?并求出这个结果.
查看答案和解析>>
科目: 来源:安徽省2017-2018学年七年级上学期期末统一质量检测数学试卷 题型:解答题
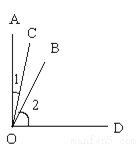
如图,∠2是∠1的4倍,∠2的补角比∠1的余角大45°.
(1)求∠1、∠2的度数;
(2)若∠AOD=90°,试问OC平分∠AOB吗?为什么?
查看答案和解析>>
科目: 来源:安徽省2017-2018学年七年级上学期期末统一质量检测数学试卷 题型:解答题
“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:
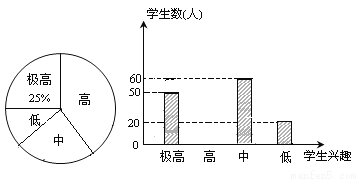
请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
(1)200人;(2)补图见解析;(3)分组后学生学习兴趣为“中”的所占的百分比为30%;对应扇形的圆心角为108°. 【解析】试题分析:(1)用“极高”的人数所占的百分比,即可解答; (2)求出“高”的人数,即可补全统计图; (3)用“中”的人数调查的学生人数,即可得到所占的百分比,所占的百分比即可求出对应的扇形圆心角的度数. 试题解析: (人). 学生学习兴趣为“高”的人...查看答案和解析>>
科目: 来源:安徽省2017-2018学年七年级上学期期末统一质量检测数学试卷 题型:解答题
星期日早晨,学校组织共青团员去参观雷锋纪念馆,小颖因故迟到没有赶上旅游车,于是她乘坐一辆出租车前往追赶,出租车司机说:“若以每小时80千米的速度,则需要1.5小时才能追上;若以每小时90千米的速度,则40分钟就能追上”.你知道出租车司机估计旅游车的速度是每小时多少千米吗?
出租车司机估计的旅游车速度是每小时72千米. 【解析】试题分析:设旅游车的速度是每小时千米,由“每小时行80千米,需1.5小时才能追上”,“每小时行90千米,40分钟就能追上”根据路程相等列出方程求解即可. 试题解析:设旅游车的速度是每小时千米,依题意得 , 解得. 答:出租车司机估计的旅游车速度是每小时72千米.查看答案和解析>>
科目: 来源:安徽省2017-2018学年七年级上学期期末统一质量检测数学试卷 题型:解答题
阅读下面材料并回答问题:
点A,B在数轴上分别表示数a,b,A,B两点之间的距离表示为AB.
当A,B两点中有一点在原点时:
不妨设A在原点,如图1,AB=OB=|b|=|a-b|;
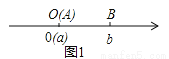
当A,B两点都不在原点时:
①如图2,点A,B都在原点的右边,AB=OB-OA=|b|-|a|=b-a=|a-b|;
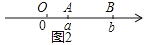
②如图3,点A,B都在原点左边,AB=OB-OA=|b|-|a|=(-b)-(-a)=|a-b|;

③如图4,点A,B在原点的两边,AB=OA+OB=|a|+|b|=a+(-b)=|a-b|;
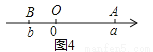
综上,数轴上A,B两点之间的距离AB=|a-b|.
(1)回答问题:数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ,数轴上表示x和-1的两点之间的距离是 .
(2)如图5,若|a-b|=2013,且OA=2OB,求a+b的值.
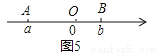
(3)结合两点之间的距离,若点M表示的数为x,当代数式|x+1|+|x-2|取最小值时,相应x的取值范围是
(1)3,3,4,|x+1|;(2)-671;(3)-1≤x≤2. 【解析】试题分析:(1)根据两点间的距离公式即可求解; (2)根据题意列出关于的方程,求出方程的解即可得到的值; (3)当大于等于0,且小于等于0时,原式取得最小值,求出这个最小值即可. 试题解析:(1)数轴上表示2和5的两点之间的距离是5?2=3,数轴上表示?2和?5的两点之间的距离是?2?(?5)=3,数轴上表...查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:单选题
从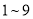 这九个自然数中任取一个,是
这九个自然数中任取一个,是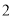 的倍数的概率是( ).
的倍数的概率是( ).
A. 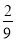 B.
B. 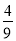 C.
C. 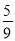 D.
D. 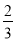
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:单选题
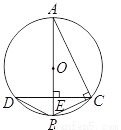
如图,已知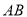 是⊙
是⊙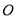 的直径,弦
的直径,弦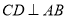 于
于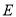 ,连接
,连接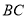 、
、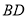 、
、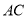 ,下列结论中不一定正确的是( ).
,下列结论中不一定正确的是( ).
A. 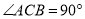 B.
B. 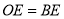 C.
C. 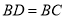 D.
D. 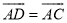
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:单选题
下列说法正确的是( ).
A. 半圆是弧,弧也是半圆 B. 三点确定一个圆
C. 平分弦的直径垂直于弦 D. 直径是同一圆中最长的弦
D 【解析】试题解析:A、半圆是弧,但弧不一定是半圆,故本选项错误; B、不在同一直线上的三点确定一个圆,故本选项错误; C、当被平分的弦为直径时,两直径不一定垂直,故本选项错误; D、直径是同一圆中最长的弦,故本选项正确, 故选D.查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:单选题
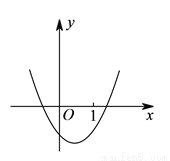
“已知二次函数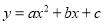 的图像如图所示,试判断
的图像如图所示,试判断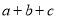 与
与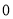 的大小.”一同学是这样回答的:“由图像可知:当
的大小.”一同学是这样回答的:“由图像可知:当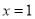 时
时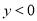 ,所以
,所以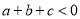 .”他这种说明问题的方式体现的数学思想方法叫做( ).
.”他这种说明问题的方式体现的数学思想方法叫做( ).
A. 换元法 B. 配方法 C. 数形结合法 D. 分类讨论法
C 【解析】试题解析:由解析式可推出,x=1时y=a+b+c; 然后结合图象可以看出x=1时对应y的值小于0,所以可得a+b+c<0. 解决此题时将解析式与图象紧密结合,所以解决此题利用的数学思想方法叫做数形结合法. 故选C.查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:单选题
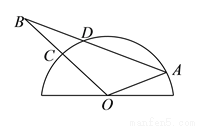
如图,半圆 是一个量角器,
是一个量角器, 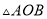 为一纸片,
为一纸片, 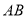 交半圆于点
交半圆于点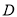 ,
, 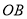 交半圆于点
交半圆于点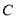 ,若点
,若点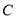 、
、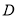 、
、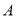 在量角器上对应读数分别为
在量角器上对应读数分别为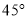 ,
, 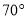 ,
, 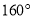 ,
, 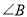 的度数为( ).
的度数为( ).
A. 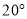 B.
B. 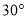 C.
C. 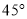 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com