
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(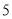 分)先化简,后求值:
分)先化简,后求值:
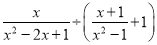 ,其中
,其中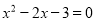 .
.
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(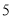 分)如图,在
分)如图,在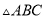 中,
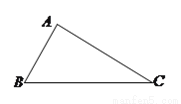
中, 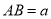 ,
, 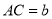 .请用尺规作一条直线
.请用尺规作一条直线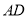 ,使其将
,使其将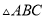 面积分为
面积分为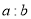 两部分.(保留作图痕迹,不写作法)
两部分.(保留作图痕迹,不写作法)
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
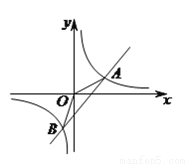
(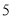 分)如图,一次函数
分)如图,一次函数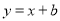 的图象与反比例函数
的图象与反比例函数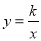 图象交于
图象交于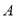 ,
, 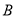 两点,点
两点,点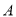 的坐标为
的坐标为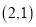 .
.
(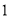 )求一次函数和反比例函数的表达式.
)求一次函数和反比例函数的表达式.
(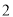 )求
)求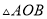 的面积.
的面积.
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(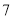 分)如图,点
分)如图,点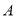 、
、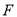 、
、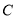 、
、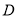 在同一直线上,点
在同一直线上,点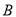 、
、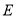 分别在直线
分别在直线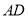 的两侧,且
的两侧,且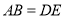 ,
, 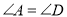 ,
, 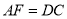 .
.
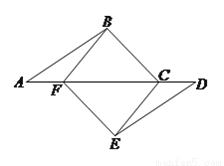
(1)求证:四边形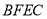 是平行四边形.
是平行四边形.
(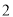 )要使四边形
)要使四边形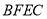 为矩形,需要添加一个条件.你可以添加下列条件中的__________.(无需证明)
为矩形,需要添加一个条件.你可以添加下列条件中的__________.(无需证明)
①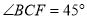
②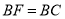
③连接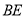 ,
, 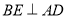
④连接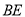 ,
, 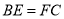
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(本题满分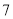 分)小明、小华在一栋高楼前感慨楼房真高.小明说:“这楼起码
分)小明、小华在一栋高楼前感慨楼房真高.小明说:“这楼起码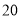 层!”小华却不以为然:“
层!”小华却不以为然:“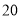 层?我看没有!”小明说:“有本事,就让我们一起来测量吧!”
层?我看没有!”小明说:“有本事,就让我们一起来测量吧!”
如图,矩形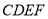 表示楼体,小明、小华在楼体两侧各选
表示楼体,小明、小华在楼体两侧各选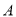 、
、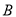 两点,使得
两点,使得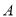 、
、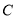 、
、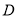 、
、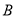 四点在同一直线上,利用皮尺和侧倾器测得如下数据,
四点在同一直线上,利用皮尺和侧倾器测得如下数据, 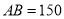 米,
米, 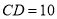 米,
米, 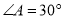 ,
, 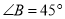 .
.
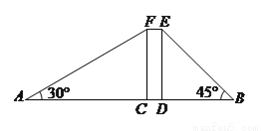
( )请你帮助他们算一算楼高.(结果保留根号)
)请你帮助他们算一算楼高.(结果保留根号)
( )若每层楼按
)若每层楼按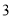 米计算,你支持小明还是小华的观点呢?请说明理由.
米计算,你支持小明还是小华的观点呢?请说明理由.
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
( 分)某超市对进货价为
分)某超市对进货价为 元/千克的某种苹果的销售情况进行统计,发现每天销售量
元/千克的某种苹果的销售情况进行统计,发现每天销售量 (千克)与销售价
(千克)与销售价 (元/千克)存在一次函数关系,如图.
(元/千克)存在一次函数关系,如图.

( )求
)求 关于
关于 的函数关系式.
的函数关系式.
( )应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(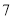 分)周末,小英与她的父亲、母亲计划从西安外出旅游,初步选择了位于西安东线的景点
分)周末,小英与她的父亲、母亲计划从西安外出旅游,初步选择了位于西安东线的景点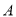 :兵马俑,
:兵马俑, 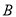 :华山,以及位于西线的景点
:华山,以及位于西线的景点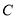 :太白山,
:太白山, 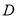 :法门寺,
:法门寺, 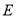 :杨凌现代农业示范园.由于时间仓促,他们只能去其中的两个景点,并且希望两个景点能位于一条线路上.到底去哪两个景点,三人意见不统一.在这种情况下,小英父亲建议,用小英学过的摸卡片游戏来决定.规则如下:在五个背面完全相同的卡片上写上五个景点的代号,然后洗匀,背面朝上放在桌面上,让小英随机摸出一张,不放回,然后让小英母亲再随机摸出一张.照上面的规则,请你解答下列问题:
:杨凌现代农业示范园.由于时间仓促,他们只能去其中的两个景点,并且希望两个景点能位于一条线路上.到底去哪两个景点,三人意见不统一.在这种情况下,小英父亲建议,用小英学过的摸卡片游戏来决定.规则如下:在五个背面完全相同的卡片上写上五个景点的代号,然后洗匀,背面朝上放在桌面上,让小英随机摸出一张,不放回,然后让小英母亲再随机摸出一张.照上面的规则,请你解答下列问题:
(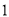 )己知小英的理想旅游景点是兵马俑,求小英摸出写有
)己知小英的理想旅游景点是兵马俑,求小英摸出写有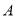 的卡片的概率.
的卡片的概率.
(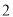 )求小英和母亲摸出的景点位于一条线上(东线或西线)的概率.
)求小英和母亲摸出的景点位于一条线上(东线或西线)的概率.
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
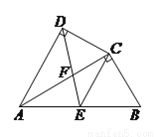
(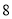 分)如图,在四边形
分)如图,在四边形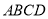 中,
中, 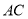 平分
平分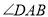 ,
, 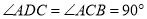 ,
, 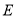 为
为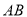 的中点,连接
的中点,连接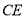 、
、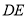 ,
, 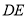 交
交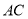 于点
于点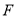 .
.
( )求证:
)求证: 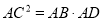 .
.
(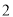 )若
)若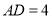 ,
, 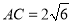 ,求
,求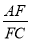 的值.
的值.
查看答案和解析>>
科目: 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
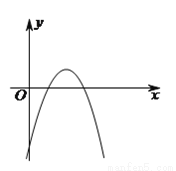
(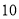 分)如图,抛物线
分)如图,抛物线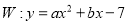 的顶点为
的顶点为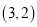 .
.
(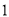 )求抛物线
)求抛物线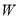 的函数表达式.
的函数表达式.
(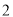 )若抛物线形
)若抛物线形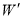 与
与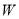 关于
关于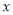 轴对称,求抛物线
轴对称,求抛物线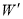 的函数表达式.
的函数表达式.
(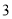 )在(
)在(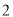 )的基础上,设
)的基础上,设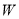 上的点
上的点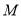 、
、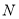 始终与
始终与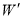 上的点
上的点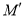 、
、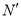 分别关于
分别关于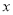 轴对称,是否存在点
轴对称,是否存在点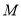 、
、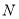 (
(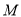 、
、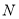 分别位于抛物线对称轴两侧,且
分别位于抛物线对称轴两侧,且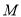 在
在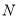 的左侧),使四边形
的左侧),使四边形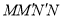 为正方形?
为正方形?
若存在,求出点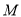 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com