
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:填空题
若分式方程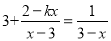 无解,则k=__________
无解,则k=__________
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
(1)分解因式:① 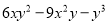 , ②
, ②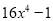 ;
;
(2)已知a+b=2,求 的值.
的值.
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
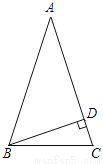
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
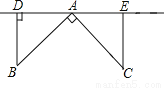
如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
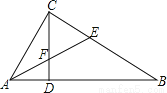
如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC、CD于E、F.试说明△CEF是等腰三角形.
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
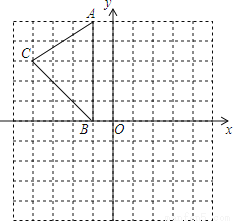
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标;
(3)在y轴上画出点P,使PA+PC最小;
(4)求六边形AA1C1B1BC的面积..
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
(1)甲的平均攀登速度是12米/分钟;(2)倍. 【解析】试题分析:(1)根据题意可以列出相应的分式方程,从而可以求得甲的平均攀登速度; (2)根据(1)中甲的速度可以表示出丙的速度,再用甲的速度比丙的平均攀登速度即可解答本题. 试题解析::(1)设乙的速度为x米/分钟, , 解得,x=10, 经检验,x=10是原分式方程的解, ∴1.2x=12, ...查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
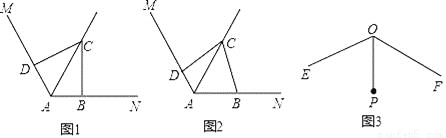
已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个 ②3个 ③4个 ④4个以上
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:单选题
若∠A=25°18′,∠B=25°19′1″,∠C=25.31°,则( )
A. ∠A>∠B>∠C B. ∠B>∠A>∠C
C. ∠B>∠C>∠A D. ∠C>∠B>∠A
C 【解析】试题分析:1°=60′,1′=60″,∠C=25.31°=25°18′36″,则∠B〉∠C〉∠A,故选择C.查看答案和解析>>
科目: 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:单选题
如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
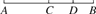
A. CD=AC-BD B. CD=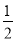 BC C. CD=
BC C. CD=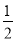 AB-BD D. CD=AD-BC
AB-BD D. CD=AD-BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com