
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:填空题
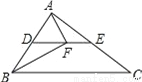
如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为_____.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:填空题
如图,在平面直角坐标系中,四边形OABC是平行四边形,O(0,0),A(1,-2),B(3,1)则C点坐标为 .
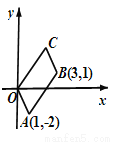
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:填空题
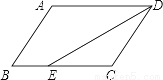
如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=________cm.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:填空题
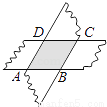
如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:填空题
若矩形两对角线的夹角为60°,且对角线长为4,则该矩形的长是________ .
【解析】∵四边形ABCD是矩形, ∴OA=OB=×4=2, ∵两对角线的夹角∠AOB=60°, ∴△AOB是等边三角形, ∴AB=OA=2, 在Rt△ABC中,矩形的长BC==2, 故答案为:2.查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:填空题
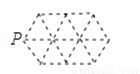
如图,在10个边长都为1的小正三角形的网格中,点P是网格的一个顶点,以点P为顶点作格点平行四边形(即顶点均在格点上的四边形),请你写出所有可能的平行四边形的对角线的长________
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:解答题
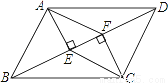
如图,在?ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断四边形AECF是不是平行四边形,并说明理由.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:解答题
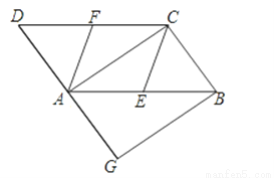
如图,在?ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:解答题
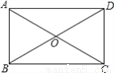
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:解答题
(1)如图,纸片?ABCD中,AD=5,S?ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图,在(1)中的四边形纸片AEE/D中,在EE/上取一点F,使EF=4,剪下△AEF,将它平移至△DE/F/的位置,拼成四边形AFF/D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
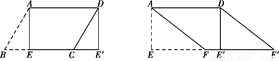
图1 图2
(1)C;(2)①证明见解析;②,3 【解析】试题分析:(1)如图1,纸片?ABCD中,AD=5,S?ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为矩形,故选:C; (2)①证明:∵纸片?ABCD中,AD=5,S?ABCD=15,过点A作AE⊥BC,垂足为E,∴AE=3.如图2: ∵△...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com