
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
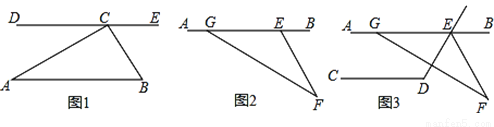
已知任意三角形ABC,
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
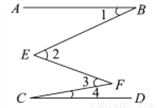
如图,已知∠1=250,∠2=450, ∠3=300,∠4=100.求证:AB//CD.
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
如图,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明。
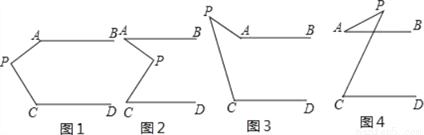
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是: .
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是: .
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是: .
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是: .
(5)在图 中,求证: .
答案见解析 【解析】试题分析:(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案; (2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案; (3)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案; (4)由AB∥CD,根据...查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
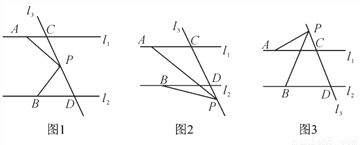
如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P.
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试直接写出∠PAC,∠APB,∠PBD之间的关系,不必写理由.
查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
要使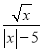 有意义,则字母
有意义,则字母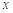 应满足的条件是( )
应满足的条件是( )
A. x≥0 B. x≠±5 C. x≥0且x≠5 D. x>0且x≠5
C 【解析】试题解析:根据题意,得, 解得x≥0,且x≠5. 故选C.查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
下列等式一定成立的是( )
A. 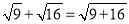 B.
B. 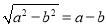
C. 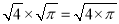 D.
D. 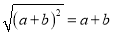
查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
矩形具有而平行四边形不一定具有的性质是( )
A. 对角相等 B. 对边相等
C. 对角线相等 D. 对角线互相平分
C 【解析】试题解析:矩形的 对角线相等,而平行四边形的对角线不一定相等. 故选C.查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
下列说法中,不正确是( )
A. 对角线互相平分的四边形是平行四边形
B. 两组对角分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边平行另一组对边相等的四边形是平行四边形
D 【解析】由平行四边形的判定方法得出A、B、C正确;即可得出结论. 【解析】 ∵对角线互相平分的四边形是平行四边形, ∴A正确; ∵两组对角分别相等的四边形是平行四边形, ∴B正确; ∵一组对边且相等的四边形是平行四边形, ∴C正确; ∵一组对边平行另一组对边相等的四边形是等腰梯形,不一定是平行四边形, ∴D不正确. 故选:D. ...查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
下列条件中,不能判断四边形ABCD是平行四边形的是( )
A. ∠A=∠C,∠B=∠D B. AB∥CD,AB=CD C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
C 【解析】试题解析:如图:、 A、∵∠A=∠C,∠B=∠D,∴四边形ABCD是平行四边形,正确,故本选项错误; B、∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,正确,故本选项错误; C、根据AB=CD,AD∥BC可能得出四边形是等腰梯形,不一定推出四边形ABCD是平行四边形,错误,故本选项正确; D、∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形...查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
在Rt△ABC中,a,b为直角边,c为斜边.若a+b=21,c=15,则△ABC的面积是( )
A. 25 B. 54 C. 63 D. 无法确定
B 【解析】试题解析:∵a+b=21,c=15, ∴(a+b)2=441,即a2+b2+2ab=441, 又∵a2+b2=c2=225, ∴2ab=216, ∴ab=54, 即S△ABC=54. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com