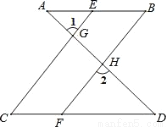
如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．请说明理由

试题见解析. 【解析】试题分析：先根据∠1=∠2，∠1=∠4得出∠2=∠4，故EC∥BF，由平行线的性质得出∠C=∠3，故可得出∠B=∠3，所以AB∥CD． 试题解析：如图， ∵∠1=∠2，∠1=∠4， ∴∠2=∠4， ∴EC∥BF， ∴∠C=∠3， ∵∠B=∠C， ∴∠B=∠3， ∴AB∥CD．

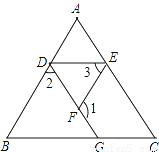
如图，已知∠1+∠2=180°，∠B=∠3，你能判断∠C与∠AED的大小关系吗？并说明理由．

∠C与∠AED相等 【解析】试题分析：∠C与∠AED相等．由邻补角定义得到∠1与∠DFE互补，再由已知∠1与∠2互补，根据同角的补角相等可得出∠2与∠DFE相等，根据内错角相等，两直线平行，得到AB与EF平行，再根据两直线平行，内错角相等可得出∠3与∠ADE相等，由已知∠B与∠3相等，利用等量代换可得出∠B与∠ADE相等，根据同位角相等，两直线平行，得到DE与BC平行，再根据两直线平行，同位...

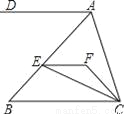
如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=120°，∠ACF=20°，求∠FEC的度数．

∠FEC=20°． 【解析】试题分析：根据AD∥BC，∠DAC=120°可得:∠ACB=60°，根据∠ACF=20°可得：∠BCF=40°，根据角平分线的性质可得：∠BCE=20°，根据EF∥BC可得：∠FEC=∠BCE=20°.

已知任意三角形ABC，

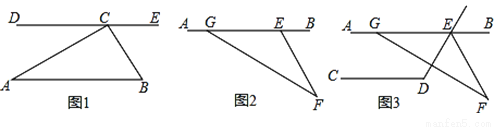
（1）如图1，过点C作DE∥AB，求证：∠DCA=∠A；

（2）如图1，求证：三角形ABC的三个内角（即∠A、∠B、∠ACB）之和等于180°；

（3）如图2，求证：∠AGF=∠AEF+∠F；

（4）如图3，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=150°，求∠F．

（1）证明见解析（2）三角形的内角和为180°（3）∠AGF=∠AEF+∠F（4）29.5 【解析】试题分析：（1）根据平行线的性即可得到结论； （2）因为平角为180°，若能运用平行线的性质，将三角形三个内角集中到同一顶点，并得到一个平角，问题即可解决； （3）根据平角的定义和三角形的内角和定理即可得到结论； （4）根据平行线的性质得到∠DEB=119°，∠AED=61°...

探究题：

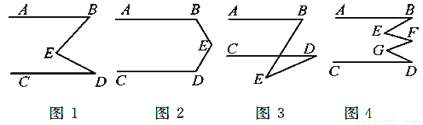
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗？

(2)若将点E移至图2的位置,此时∠B，∠D，∠E之间有什么关系？

(3)若将点E移至图3的位置,此时∠B，∠D，∠E之间的关系又如何？

(4)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系？

（1）相等（2）∠B+∠D+∠E=360°（3）∠B=∠D+∠E（4）相等 【解析】试题分析：（1）过点E作EF∥AB，由平行线的性质可知∠B=∠BEF，∠D=∠DEF，再由角之间的关系即可得出结论； （2）过点E作EF∥AB，由平行线的性质可知∠B+∠BEF=180°，∠D+∠DEF=180°，再由角之间的关系即可得出结论； （3）过点E作EF∥AB，由平行线的性质可知∠B=∠...

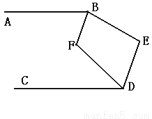
如图，已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E = 140º，求∠BFD的度数.

110° 【解析】试题分析：过点E作EG∥AB，根据平行线的性质可得∠ABE+∠BEG=180°，∠GED+∠EDC=180°，根据角的计算以及角平分线的定义可得∠FBE+∠EDF=（∠ABE+∠CDE）÷2=110°，再依据四边形内角和为360°结合角的计算即可得出结论． 试题解析：【解析】 过点E作EG∥AB，如图所示： ∴∠ABE+∠BEG=180°．∵AB∥CD，EG∥...

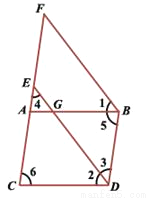
已知：如图，∠1 =∠2，∠3 =∠4，∠5 =∠6.求证：ED∥FB．

证明见解析. 【解析】试题分析：因为∠3=∠4，所以CA∥BD，由两直线平行，同旁内角互补可得∠6+∠2+∠3 = 180°，又因∠6 =∠5，∠2 =∠1，根据等量代换可得∠5+∠1+∠3 = 180°，从而根据同旁内角互补，两直线平行得出ED∥FB． 试题解析： ∵ ∠3 =∠4,∴ AC∥BD.∴ ∠6+∠2+∠3 = 180° ∵ ∠6 =∠5，∠2 =∠1,∴ ∠...

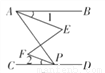
如图，∠BAP+∠APD=180°，∠1=∠2． 求证：∠E=∠F

证明见解析. 【解析】试题分析：根据已知可得出AB∥CD，进而由∠1=∠2可证得∠FPA=∠EAP，故能得出AE∥FP，即能推出要证的结论成立． 试题解析：证明：∵∠BAP+∠APD=180°（已知）， ∴AB∥CD（同旁内角互补，两直线平行）， ∴∠BAP=∠APC（两直线平行，内错角相等）， 又∵∠1=∠2（已知）， ∴∠FPA=∠EAP， ∴AE∥P...

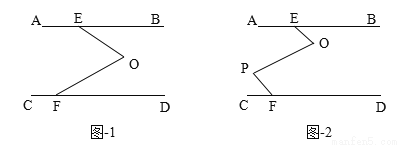
如图1，AB∥CD，EOF是直线AB、CD间的一条折线.

（1）说明：∠O=∠BEO+∠DFO.

（2）如果将折一次改为折二次，如图-2，则∠BEO、∠O、∠P、∠PFC会满足怎样的关系，证明你的结论.

证明见解析 【解析】试题分析：（1）过O作OM∥AB，根据平行线性质推出∠BEO=∠MOE，∠DFO=∠MOF，相加即可求出答案； （2）过O作OM∥AB，PN∥AB，根据平行线性质求出∠BEO=∠EOM，∠PFC=∠NPF，∠MOP=∠NPO，代入求出即可． 试题解析：（1）证明：过O作OM∥AB，∵AB∥CD，∴AB∥OM∥CD，∴∠BEO=∠MOE，∠DFO=∠MOF，∴∠...

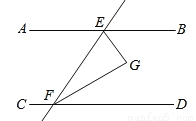
如图,直线AB∥CD，直线AB、CD被直线EF所截，EG平分∠BEF，FG平分∠DFE，

（1）若∠AEF=50°，求∠EFG的度数．

（2）判断EG与FG的位置关系，并说明理由．

（1）25°；（2）EG⊥FG 【解析】试题分析：.【解析】 （！）∵AB∥CD ∴∠EFD=∠AEF=50° ∵FG平分∠DFE ∵∠EFG=∠DFE＝×50°＝25° （2）EG⊥FG 理由：∵AB∥CD ∴∠BEF+∠EFD=180° ∵EG平分∠BEF，FG平分∠DFE ∴∠GEF=∠BEF，∠GFE=∠DFE ∴∠GEF+∠G...