已知Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D是AB中点，点E是直线AC上一点，若以C、D、E为顶点的三角形与△ABC相似，则AE的长度为_____．

3或 【解析】∵∠ACB=90°,AC=6,BC=8, ∴AB=62+82=10, ∵点D是AB中点, ∴CD=5, ∵CD=AD, ∴∠A=∠ACD, ∴C,D,E为顶点的三角形与△ABC相似，应分△ABC∽△CDE和△ABC∽△CED两种情况进行讨论: 当△ABC∽△CDE时: , 则,即CE=3,得到:AE=3, 当△ABC∽△CE...

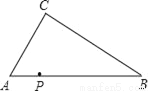
如图，点P是Rt△ABC斜边AB上的任意一点（A、B两点除外），过点P作一条直线，使截得的三角形与Rt△ABC相似，这样的直线可以作_____条．

3 【解析】 过点P分别作三边的垂线,所得△ADP, △AEP, △BPF与RtΔABC相似. 所以这样的直线能做三条.

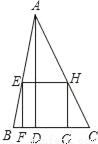
如图，△ABC的内接正方形EFGH中，EH∥BC，其中BC=4，高AD=6，则正方形的边长为_____．

【解析】∵EH∥BC, ∴△AEH∽△ABC, 设正方形的边长为x,则: , 解得x=2.4, 故答案为2.4.

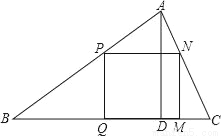
如图△ABC中，边BC=12cm，高AD=6cm，边长为x的正方形PQMN的一边在BC上，其余两个顶点分别在AB、AC上，则正方形的边长x=_____cm．

4 【解析】试题解析：如图所示： 由题意可得： 则 即： 解得： 故答案为：

确定图中路灯灯泡的位置，并画出小赵在灯光下的影子．

见解析 【解析】试题分析：根据中心投影的特点可知，连接物体和它影子的顶端所形成的直线必定经过点光源．所以分别把已知影长的两个人的顶端和影子的顶端连接并延长可交于一点，即点光源的位置，再由点光源出发连接小赵顶部的直线与地面相交即可找到小赵影子的顶端． 【解析】

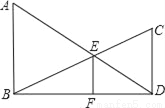
已知：如图，AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明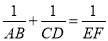成立（不要求考生证明）．

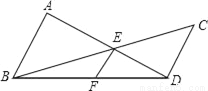
若将图中的垂线改为斜交，如图，AB∥CD，AD，BC相交于点E，过点E作EF∥AB交BD于点F，则：

（1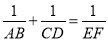）还成立吗？如果成立，请给出证明；如果不成立，请说明理由；

（2）请找出S△ABD，S△BED和S△BDC间的关系式，并给出证明．

（1）成立（2） 【解析】试题分析: （1）∵ AB∥EF,所以,∵CD∥EF,∴, ∴=1,∴, （2）分别过A作AM⊥BD于M,过E作EN⊥BD于N,过C作CK⊥BD交BD的延长线于K,由题设可得: ,∴,又∵•BD•AM=S△ABD, =S△BCD ∴BD•EN=S△BED,∴. 试题解析:（1）成立． 证明：∵ AB∥EF, 所以, ∵CD∥...

列出下列问题中的函数关系式，并判断它们是否为反比例函数．

（1）某农场的粮食总产量为1 500t，则该农场人数y（人）与平均每人占有粮食量x（t）的函数关系式；

（2）在加油站，加油机显示器上显示的某一种油的单价为每升4.75元，总价从0元开始随着加油量的变化而变化，则总价y（元）与加油量x（L）的函数关系式；

（3）小明完成100m赛跑时，时间t（s）与他跑步的平均速度v（m/s）之间的函数关系式．

（1）y=是反比例函数；（2）y=4.75x是正比例函数；（3）t=是反比例函数 【解析】试题分析: （1）由平均数,得x=，即y=是反比例函数, （2）由单价乘以油量等于总价,得y=4.75x,即y=4.75x是正比例函数, （3）由路程与时间的关系,得t=,即t=是反比例函数． 试题解析:（1）由平均数,得x=，即y=是反比例函数, （2）由单价乘以油量等于总价,...

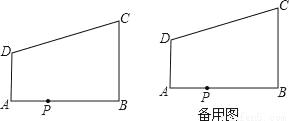
如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，求AP的长．

AP=或AP=2或AP=6 【解析】试题分析:由AD//BC, ∠B=90°,可证∠PAD=∠PBC=90°, 又由AB=8,AD=3,BC=4,设AP的长为x,则BP长为8-x,然后分别从APD∽△BPC与△APD∽△BCP去分析,利用相似三角形的对应边成比例求解即可求得答案. 试题解析:∵ AB⊥BC, ∴ ∠B=90°, ∵ AD∥BC, ∴ ∠A=180°﹣∠...

小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.

（1）如图①，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为 .

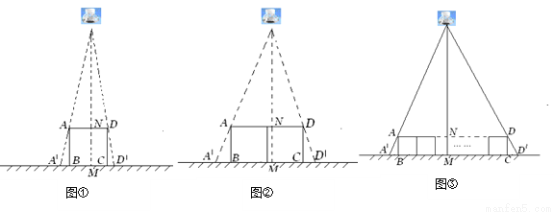（2）不改变①中灯泡的高度，将两个边长为30cm的正方形框架按图②摆放，请计算此时横向影子A′B，D′C的长度和为多少？

（3）有n个边长为a的正方形按图③摆放，测得横向影子A′B，D′C的长度和为b,求灯泡离地面的距离.（写出解题过程，结果用含a,b,n的代数式表示）

（1）180cm （2）12 cm (3) 【解析】试题分析：（1）设灯泡的位置为点P，易得△PAD∽△PA′D′，设出所求的未知数，利用相似三角形的对应边的比等于对应高的比，可得灯泡离地面的高度； （2）同法可得到横向影子A′B，D′C的长度和； （3）按照相应的三角形相似，利用相似三角形的对应边的比等于对应高的比，用字母表示出其他线段，即可得到灯泡离地面的距离． 【解析...

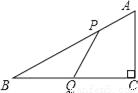
如图，在△ABC中，∠C=90°，AB=10，BC=8，P、Q分别是AB、BC边上的点，且AP=BQ=a （其中0＜a＜8）．

（1）若PQ⊥BC，求a的值；

（2）若PQ=BQ，把线段CQ绕着点Q旋转180°，试判别点C的对应点C’是否落在线段QB上？请说明理由．

（1）（2）点C′不落在线段QB上 【解析】试题分析: （1）∵∠B=∠B,∠PQB=∠C=90°∴△BQP∽△BCA, ∴,,解得：a=, (2) 作QH⊥AB于H,∵PQ=BQ,∴BH=HP,∵∠B=∠B,∠BHQ=∠C,∴△BQH∽△BAC, ∴BH:BC=BQ:AB可得: （10﹣a）:a=8:10,解得a=,CQ=（8﹣a）=, ∴BQ＜QC,∴点C′不落在...