
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
如图,AC是?ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
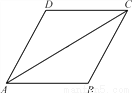
(2)若AB=2,AC=2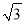 ,求?ABCD的面积.
,求?ABCD的面积.
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
(1)证明见解析;(2)12. 【解析】 试题分析:(1)利用三线合一定理可以证得∠ADB=90°,根据矩形的定义即可证得; (2)利用勾股定理求得BD的长,然后利用矩形的面积公式即可求解. 试题解析: (1)∵AB=AC,AD是BC的边上的中线, ∴AD⊥BC, ∴∠ADB=90°, ∵四边形ADBE是平行四边形. ∴平行四边形ADBE是矩形; ...查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
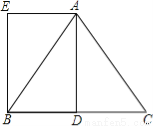
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(1)证明见解析(2)GE=BE+GD成立 【解析】试题分析:(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF; (2)由(1)得CE=CF,∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE...查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.
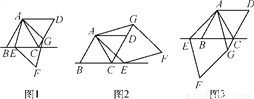
(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.
(1)AB=CG-CE(2)AB=CE-CG 【解析】试题分析:(1)根据菱形的性质可得AC=AD,AE=AG,然后证明∠DAG=∠CAE,可利用SAS证明△ACE≌△ADG,根据全等三角形的性质可得CE=DG,再根据线段的和差关系和等量代换可得答案; (2)方法与(1)类似可证明△ACG≌△ABE,进而得到BE=CG,然后可得AB=CE﹣CG. 试题解析:(1)AB=CG-CE...查看答案和解析>>
科目: 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
有同一三角形地块的甲,乙两地图,比例尺分别为1:100和1:500,那么甲地图与乙地图表示这一块的三角形面积比是( )
A. 25:1 B. 5:1 C. 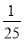 D.
D. 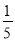
查看答案和解析>>
科目: 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
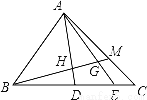
A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
D 【解析】连接EM, ∵CE:CD=CM:CA=1:3 ∴EM平行于AD ∴△BHD∽△BME,△CEM∽△CDA ∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3 ∴AH=(3﹣)ME, ∴AH:ME=12:5 ∴HG:GM=AH:EM=12:5 设GM=5k,GH=12k, ∵BH:HM=3:2=BH:17k ...查看答案和解析>>
科目: 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
如图,E、F分别在矩形ABCD的边CD、AB上,EF⊥AB,G、H分别是BC、EF的中点,EH>HG,除矩形EFBC外,图中4个矩形都彼此相似,若BC=1,则AB等于( )
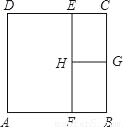
A. 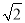 B.
B. 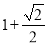 C.
C. 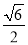 D.
D. 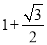
查看答案和解析>>
科目: 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
如图,矩形ABCD中,已知点M是线段AB的黄金分割点,且AM>BM,AD=AM,FB=BM,EF和GM把矩形ABCD分成四个小矩形,其面积分别用S1,S2,S3,S4表示,EF与MG相交与点N,则以下结论正确的有( )
①N是GM的黄金分割点 ②S1=S4③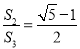 .
.
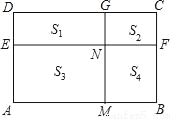
A. ①② B. ①③ C. ③ D. ①②③
A 【解析】因为四边形ABCD是矩形,AM=AD,BM=BF, 所以四边形AMGD,四边形BMNF都是正方形, 所以AM=AD=MG=BC,MB-BF=MN=FN, 因为点M是线段AB的黄金分割点,AM>BM, 所以, 所以, 所以,故②正确, 所以, 所以N是GM的黄金分割点,故①正确, 因为, 因为, 所以,故③错误, ...查看答案和解析>>
科目: 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. 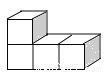 B.
B. 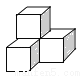 C.
C. 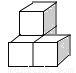 D.
D. 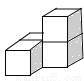
查看答案和解析>>
科目: 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
将x=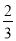 代入反比例函数y=﹣
代入反比例函数y=﹣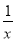 中,所得函数记为y1,又将x=y1+1代入函数中,所得函数记为y2,再持x=y2+1代入函数中,所得函数记为y3,如此继续下去,则y2009值为( )
中,所得函数记为y1,又将x=y1+1代入函数中,所得函数记为y2,再持x=y2+1代入函数中,所得函数记为y3,如此继续下去,则y2009值为( )
A. 2 B. -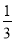 C.
C. 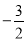 D.
D. 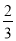
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com