
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
如图,把矩形纸片ABCD沿对角线BD折叠,设重叠部分为△EBD,则下列说法错误的是( )
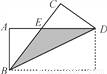
A. AB=CD B. ∠BAE=∠DCE C. EB=ED D. ∠ABE一定等于30°
D 【解析】试题分析:根据ABCD为矩形,所以∠BAE=∠DCE,AB=CD,再由对顶角相等可得∠AEB=∠CED,所以△AEB≌△CED,就可以得出BE=DE,由此判断即可. 【解析】 ∵四边形ABCD为矩形 ∴∠BAE=∠DCE,AB=CD,故A、B选项正确; 在△AEB和△CED中, , ∴△AEB≌△CED(AAS), ∴BE=DE,故C正确; ...查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
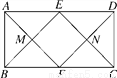
A. 正方形 B. 菱形 C. 矩形 D. 无法确定
A 【解析】∵四边形ABCD为矩形, ∴AD∥BC,AD=BC, 又∵E,F分别为AD,BC中点, ∴AE∥BF,AE=BF,ED∥CF,DE=CF, ∴四边形ABFE为平行四边形,四边形BFDE为平行四边形, ∴BE∥FD,即ME∥FN, 同理可证EN∥MF, ∴四边形EMFN为平行四边形, ∵四边形ABFE为平行四边形,∠ABC为直角, ...查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图1,测得AC=2,当∠B=60°时,如图2,AC=( )
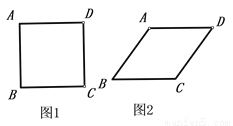
A. 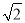 B. 2 C.
B. 2 C. 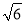 D. 2
D. 2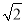
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
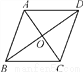
如图,在菱形ABCD中,AC,BD相交于点O,若∠BCO=55°,则∠ADO=____________.
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
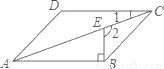
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为__.
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
如图,矩形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,则DE的长为____________.
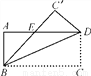
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是 (写出一个即可).
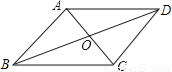
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是_____.
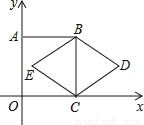
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .
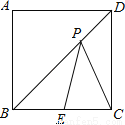
查看答案和解析>>
科目: 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
(1)请写出图中两对全等的三角形;
(2)求证:四边形BCEF是平行四边形.
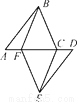
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com