
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
若直线y=m(m为常数)与函数y= 的图象恒有三个不同的交点,则常数m的取值范围是_____.
的图象恒有三个不同的交点,则常数m的取值范围是_____.
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
弦AB将⊙O分成度数之比为1:5的两段弧,则∠AOB=________°.
60 【解析】试题解析:∵弦AB将圆分成的两段弧所对的圆心角度数之比为1:5, ∴∠AOB=×360°=60°, 故答案为:60.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为_____.
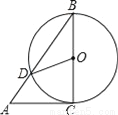
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
如图,在直角坐标系中,四边形OABC是直角梯形,BC∥OA,⊙P分别与OA、OC、BC相切于点E、D、B,与AB交于点F.已知A(2,0),B(1,2),则tan∠FDE=________.
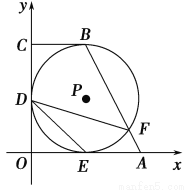
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
如图,⊙O中OA⊥BC,∠CDA=25°,则∠AOB的度数为________.
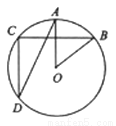
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm.求:⊙O的半径.
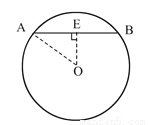
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:解答题
已知二次函数y=2x2﹣4mx+m2+2m(m是常数).
(1)求该函数图象的顶点C的坐标(用含m的代数式表示);
(2)当m为何值时,函数图象的顶点C在二、四象限的角平分线上?
(1)(m,﹣m2+2m);(2)m为0或3时 【解析】试题分析:(1)根据顶点坐标公式直接计算即可; (2)根据点C坐标,点C在直线y=-x上,即使横纵坐标互为相反数,计算即可得出答案. 试题解析:(1)由y=2x2-4mx+m2+2m =2(x2-2mx)+m2+2m =2(x-m)2-m2+2m, 得顶点C的坐标为(m,-m2+2m); (2)点C坐标(m,2m-...查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:解答题
(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。
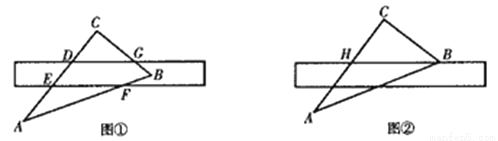
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
(1)∠CEF=48°; (2)BC的长为6.96m. 【解析】试题分析:(1)由DG//EF,可知要求∠CEF的度数,需求出∠CDG的度数,而在△CDG在,∠C=90°,∠CGD=42°,从而得解. (2)由已知可得∠CBH=42°,由三角函数即可得; 试题解析:(1)∵ ∠CGD=42°,∠C=90°,∴ ∠CDG=90°- 42°=48°,∵ DG∥EF, ∴∠CEF...查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷二 题型:解答题
已知抛物线 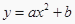 过点(
过点( 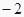 ,
,  )和点(1,6),
)和点(1,6),
(1)求这个函数解析式;
(2)当x为何值时,函数y随x的增大而减小;
(1);(2)x>0 【解析】试题分析:(1)利用待定系数法即可求出函数的关系式. (2)由开口及对称轴即可判定出当为何值时,函数y随x的增大而增大. 试题解析:(1)把点(-2,-3)和点(1,6)代入y=ax2+b得 , 解得, 所以这个函数的关系式为y=-3x2+9; (2)∵这个函数的关系式为y=-3x2+9; ∴对称轴x=0, ∵a=-3<0, ∴抛物...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com