
科目: 来源:人教版八年级下册数学全册综合测试二 题型:解答题
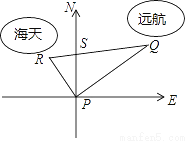
某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口 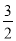 小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试二 题型:解答题
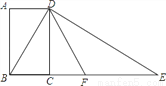
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4,设AB=x,AD=y,求x2+(y﹣4)2的值.
查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试二 题型:解答题
如图,D、E、F分别在△ABC的边BC、AB、AC上,且DE∥AF,DE=AF,G在FD的延长线上,DG=DF.试说明AG和ED互相平分.
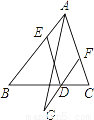
查看答案和解析>>
科目: 来源:人教版八年级下册数学全册综合测试二 题型:解答题
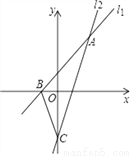
如图,直线l1、l2相交于点A(2,3),直线l1与x轴交点B的坐标为(﹣1,0),直线l2与y轴交于点C,已知直线l2的解析式为y=2.5x﹣2,结合图象解答下列问题:
(1)求直线l1的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A. 37° B. 41° C. 37°或41° D. 以上答案均不对
C 【解析】试题解析:①若3、4是直角边, ∵两直角边为3,4, ∴斜边长==5, ∴较小的锐角所对的直角边为3,则其正弦值为; ②若斜边长为4,则较小边=≈2.65, ∴较小边所对锐角正弦值约==0.6625, 利用计算器求得角约为37°或41°. 故选C.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A. 点P在⊙O上 B. 点P在⊙O内 C. 点P在⊙O外 D. 无法确定
C 【解析】试题解析:∵⊙O的半径为5,点P到圆心O的距离为6, ∴点P到圆心O的距离大于圆的半径, ∴点P在⊙O外. 故选C.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
若⊙O1、⊙O2的半径分别为4和6,圆心距O1O2=8,则⊙O1与⊙O2的位置关系是( )
A. 内切 B. 相交 C. 外切 D. 外离
B 【解析】试题分析:⊙O1、⊙O2的直径分别为4和6,圆心距O1O2=2,⊙O1、⊙O2的半径之和为5,只差为1,而1查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
在△ABC中,∠C=90°,∠A=72°,AB=10,则边AC的长约为(精确到0.1)( )
A. 9.1 B. 9.5 C. 3.1 D. 3.5
C 【解析】分析:在Rt△ABC中,根据三角函数的定义,易得AB、AC及∠A的关系,进而计算可得答案. 解答:【解析】 根据题意 在Rt△ABC中,有cosA=,sinA=; 则AC=AB?cosA=10×cos72°≈3.1; 故选C.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?( )
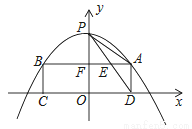
A. 始终不相似 B. 始终相似 C. 只有AB=AD时相似 D. 无法确定
B 【解析】试题分析:设A(x,-+1)根据题意可求出PA、PD、PE的值,从而得出PE:PA=PA:PD,又∠APE=∠DPA,因此,△PAD∽△PEA.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
已知⊙O的半径为r,圆心O到直线l的距离为d.若直线l与⊙O有交点,
则下列结论正确的是( )
A.d=r B.0≤d≤r C.d≥r D.d<r
B 【解析】 试题分析:圆与直线有交点,即可能为1个交点或2个交点,当时,圆与直线相切,即有一个交点,当时,有两个交点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com