
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:填空题
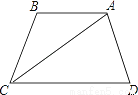
如图,AB∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=________°.
查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
(1)请在横线上填写合适的内容,完成下面的证明:
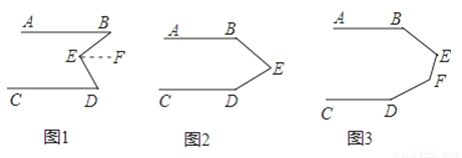
如图1,AB∥CD,求证:∠B+∠D=∠BED.
证明:过点E引一条直线EF∥AB
∴∠B=∠BEF,(___________)
∵AB∥CD,EF∥AB
∴EF∥CD(___________)
∴∠D=________(___________)
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED.
(2)如图2,AB∥CD,请写出∠B+∠BED+∠D=360°的推理过程.________
(3)如图3,AB∥CD,请直接写出结果∠B+∠BEF+∠EFD+∠D=________
查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:填空题
一个正方体中有一条棱是a,与a平行棱长有________ 条,与a垂直并相交的棱长有________ 条.
3; 4. 【解析】根据长方体的特征,12条棱分别互相平行的有3组,每组4条棱的长度相等且平行,由此可知:与a平行的棱有3条,与a相交并垂直的棱有4条. 【解析】 由分析得:与a平行的棱有3条,与a相交并垂直的棱有4条。 故答案为:3,4.查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
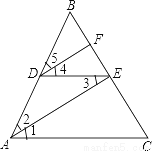
阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2(________)
∵AC∥DE(已知)
∴∠1=∠3(________)
故∠2=∠3(________)
∵DF∥AE(已知)
∴∠2=∠5(________)
∴∠3=∠4(________)
∴DE平分∠BDE(________)
查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:填空题
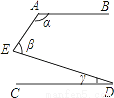
已知,如图,AB∥CD,则∠α、∠β、∠γ之间的关系为________
查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
如图,已知∠AOB和射线O′B′,用尺规作图法作∠A′O′B′=∠AOB(要求保留作图痕迹).
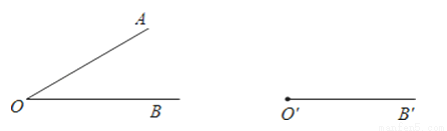
查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
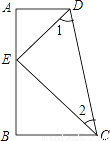
查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
如图所示,直线a∥b,AC丄AB,AC交直线b于点C,∠1=60°,求∠2的度数.
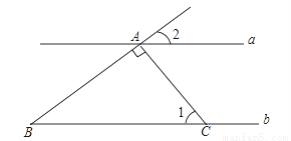
查看答案和解析>>
科目: 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
如图,已知直线AB∥DF,∠D+∠B=180°,
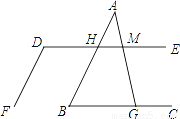
(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
(1)证明见解析;(2)105°. 【解析】(1)根据平行线的性质得出∠D+∠BHD=180°,等量代换得出∠B=∠DHB,根据平行线的判定得出即可; (2)根据平行线的性质求出∠AGB=∠AMD=75°,再根据邻补角的定义即可求出∠AGC的度数. (1)证明:∵AB∥DF, ∴∠D+∠BHD=180°, ∵∠D+∠B=180°, ∴∠B=∠DHB, ∴D...查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:期中检测卷 题型:单选题
下列各点中,在函数y=-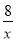 图象上的是( )
图象上的是( )
A.(﹣2,4) B.(2,4) C.(﹣2,﹣4) D.(8,1)
A 【解析】 试题分析:所有在反比例函数上的点的横纵坐标的积应等于比例系数.本题只需把所给点的横纵坐标相乘,结果是﹣8的,就在此函数图象上查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com