
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:解答题
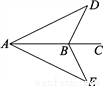
如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔D、E与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?
查看答案和解析>>
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:解答题
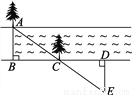
某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20步有一棵树C,继续前行20步到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长就是河宽AB.
请你说明他们做法的正确性.
查看答案和解析>>
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:单选题
把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A顶着桌面,若另两个顶点分别距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离即DE的长为( )
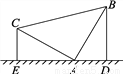
A. 4cm B. 6cm C. 8cm D. 求不出来
C 【解析】∵ ∠BAC=90° ∠AEC=90° ∴ ∠BAC=∠AEC ∵ ∠DAB+∠BAC=∠DAC ∠ECA+∠AEC=∠DAC ∠BAC=∠DEC ∴ ∠ECA=∠DAB ∵ △ABD是直角三角形 △CAE是直角三角形 AB=AC ∠ECA=∠DAB ∴ △ABD≌△CAE (一边一锐角对应相等的两个直角三角形全等) ∴ AE=BD AD=CE...查看答案和解析>>
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:单选题
把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A顶着桌面,若另两个顶点分别距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离即DE的长为( )
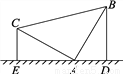
A. 4cm B. 6cm C. 8cm D. 求不出来
C 【解析】∵ ∠BAC=90° ∠AEC=90° ∴ ∠BAC=∠AEC ∵ ∠DAB+∠BAC=∠DAC ∠ECA+∠AEC=∠DAC ∠BAC=∠DEC ∴ ∠ECA=∠DAB ∵ △ABD是直角三角形 △CAE是直角三角形 AB=AC ∠ECA=∠DAB ∴ △ABD≌△CAE (一边一锐角对应相等的两个直角三角形全等) ∴ AE=BD AD=CE...查看答案和解析>>
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:填空题
某大学计划为新生配备如图①所示的折叠凳,图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30cm,则由以上信息可推得CB的长度为_____.
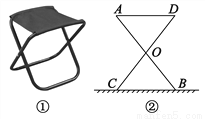
查看答案和解析>>
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:解答题
如图所示,小明为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m.你能猜出河有多宽吗?说说理由.
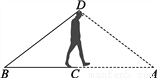
查看答案和解析>>
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:解答题
如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,你发现线段AD与BE有什么大小关系?试说明你的结论.

查看答案和解析>>
科目: 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:解答题
如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小刚想估测这两根电线杆之间的距离,于是小刚从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小刚测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
(2)如果小刚一步大约60厘米,请你求A、B两根电线杆之间的距离并简述理由.
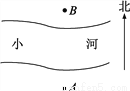
查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型:单选题
若AD是△ABC的中线,则下列结论中错误的是( )
A. AB=BC B. BD=DC C. AD平分BC D. BC=2DC
A 【解析】【解析】 ∵AD是△ABC的中线,∴AD平分BC ,∴BD=DC,BC=2DC.故A错误.故选A.查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型:单选题
三角形一边上的中线把原三角形一定分成两个( )
A. 形状相同的三角形 B. 面积相等的三角形 C. 直角三角形 D. 周长相等的三角形
B 【解析】三角形一边上的中线把原三角形一定分成两个面积相等的三角形. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com