桂林某学校从参加高三年级第二次模拟考试的学生中随机抽出100名学生，将其数学成绩(均为整数)分成五段[50，70)，[70，90)，[90，110)，[110，130)，[130，150]后得到如下部分频率分布直方图，分析图形的信息，回答下列问题：

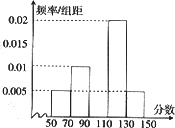
(Ⅰ)求分数在[90，110)内的频率和学生数，并补全这个频率分布直方图；

(Ⅱ)现从分数段[90，150]的学生中随机抽取2人给予助学金奖励，抽到的学生成绩在[90，110)内每人奖励100元，在[100，130)内每人奖励200元，在[130，150)内每人奖励300元，用ξ表示抽取结束后总的奖励金额，求ξ的分布列和数学期望

如图，在直四棱柱ABCD－A₁B₁C₁D₁中，底面ABCD为等腰梯形，AB∥CD，AB＝2，BC＝CD＝1，AA₁＝1，F在棱AB(不含端点)上，且C₁F与底面ABCD所成角的大小为45°

(Ⅰ)证明：直线D₁B₁⊥平面FCC₁；

(Ⅱ)求二面角B－FC₁－C的大小

在△ABC中，内角A、B、C的对边长分别为a、b、c，已知8sin²－2cos2A＝7，且a＝，b＋c＝5，求角A及△ABC的面积

已知：有穷数列{a_n}共有2k项(整数k≥2)，a₁＝2，设该数列的前n项和为S_n且满足S_n＋1＝aS_n＋2(n＝1，2，…，2k－1)，a＞1．

(1)求{a_n}的通项公式；

(2)设b_n＝log₂a_n，求{b_n}的前n项和T_n；

(3)设c_n＝，若a＝2，求满足不等式|C₁－|＋|C₂－|＋…＋|C_2k－1－|＋|C_2k－|≥时k的最小值．

已知函数f(x)＝(x∈R)．

(1)当f(1)＝1时，求函数f(x)的单调区间；

(2)设关于x的方程f(x)＝的两个实根为x₁，x₂，且－1≤a≤1，求|x₁－x₂|的最大值；

(3)在(2)的条件下，若对于[－1，1]上的任意实数t，不等式m²＋tm＋1≥|x₁－x₂|恒成立，求实数m的取值范围．

从某校高三年级800名男生中随机抽取50名学生测量其身高，据测量被测学生的身高全部在155cm到195cm之间．将测量结果按如下方式分成8组：第一组[155，160)，第二组[160，165)，……，第八组[190，195]，如下图是按上述分组得到的频率分布直方图的一部分．已知：第1组与第8组的人数相同，第6组、第7组和第8组的人数依次成等差数列．

(1)求下列频率分布表中所标字母的值，并补充完成频率分布直方图；

(2)若从身高属于第6组和第8组的所有男生中随机的抽取2名男生，记他们的身高分别为x、y，求满足：|x－y|≤5事件的概率．

已知椭圆C：＋＝1(a＞b＞0)的离心率e＝，且椭圆经过点N(2，－3)．

(1)求椭圆C的方程；

(2)求椭圆以M(－1，2)为中点的弦所在直线的方程．

如图，棱柱ABCD－A₁B₁C₁D₁的底面ABCD为菱形，平面AA₁C₁C⊥平面ABCD．

(1)证明：BD⊥AA₁；

(2)证明：平面AB₁C//平面DA₁C₁

(3)在直线CC₁上是否存在点P，使BP∥平面DA₁C₁？若存在，求出点P的位置；若不存在，说明理由．

已知：在△ABC中，a，b，c分别是角A、B、C所对的边，向量m＝(2sin，)，n＝(sin＋，1)且m·n＝．

(1)求角B的大小；

(2)若角B为锐角，a＝6，S_△ABC＝6，求b的值．

设数列{a_n}，{b_n}满足a₁＝4，a₂＝，a_n+＋1＝，b_n+1＝．

(1)用a_n表示a_n+1；并证明：n∈N_n，a_n＞2；

(2)证明：{ln}是等比数列；

(3)设S_n是数列{a_n}的前n项和，当n≥2时，S_n与2(n＋)是否有确定的大小关系？若有，加以证明；若没有，请说明理由．