四棱锥P－ABCD中，PA⊥平面ABCD，E为AD的中点，ABCE为菱形，∠BAD＝120°，PA＝AB，G，F分别是线段CE，PB上的动点，且满足＝＝λ∈(0，1)．

(Ⅰ)求证：FG∥平面PDC；

(Ⅱ)求λ的值，使得二面角F－CD－G的平面角的正切值为．

设等差数列{a_n}的首项a₁为a，前n项和为S_n．

(Ⅰ)若S₁，S₂，S₄成等比数列，求数列{a_n}的通项公式；

(Ⅱ)证明：n∈N*，S_n，S_n+1，S_n+2不构成等比数列．

在△ABC中，角A，B，C所对的边分别为a，b，c，已知tan(A＋B)＝2．

(Ⅰ)求sinC的值；

(Ⅱ)当a＝1，c＝时，求b的值．

设抛物线C₁：x²＝4y的焦点为F，曲线C₂与C₁关于原点对称．

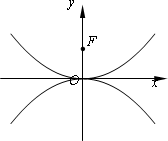
(Ⅰ)求曲线C₂的方程；

(Ⅱ)曲线C₂上是否存在一点P(异于原点)，过点P作C₁的两条切线PA，PB，切点A，B，满足|AB|是|FA|与|FB|的等差中项？若存在，求出点P的坐标；若不存在，请说明理由．

已知函数f(x)＝x³＋ax²＋bx，a，b∈R．

(Ⅰ)曲线C：y＝f(x)经过点P(1，2)，且曲线C在点P处的切线平行于直线y＝2x＋1，求a，b的值；

(Ⅱ)已知f(x)在区间(1，2)内存在两个极值点，求证：0＜a＋b＜2．

已知正四棱锥P－ABCD中，底面是边长为2的正方形，高为．M为线段PC的中点．

(Ⅰ)求证：PA∥平面MDB；

(Ⅱ)N为AP的中点，求CN与平面MBD所成角的正切值．

已知函数f(x)＝＋alnx－2(a＞0)．

(1)若曲线y＝f(x)在点P(1，f(1))处的切线与直线y＝x＋2垂直，求函数y＝f(x)的单调区间；

(2)若对于x∈(0，＋∞)都有f(x)＞2(a－1)成立，试求a的取值范围；

(3)记g(x)＝f(x)＋x－b(b∈R)．当a＝1时，函数g(x)在区间[e^－1，e]上有两个零点，

已知f(x)＝x＋asinx．

(Ⅰ)若f(x)在(－∞，＋∞)上为增函数，求实数a的取值范围；

(Ⅱ)当常数a＞0时，设g(x)＝，求g(x)在[]上的最大值和最小值．

设函数

(Ⅰ)设∠A是△ABC的内角，且为钝角，求f(A)的最小值；

(Ⅱ)设∠A，∠B是锐角△ABC的内角，且∠A＋∠B＝，f(A)＝1，BC＝2，求△ABC的三个内角的大小和AC边的长．