
 已知二次函数y=x2-2x-3
已知二次函数y=x2-2x-3分析 (1)根据顶点式求得顶点坐标,令x=0,求得与y轴的交点,令y=0,求得与x轴的坐标,再在对称轴的两侧取两组对称点,列表,然后描点、连线即可.
(2)根据二次函数的性质即可求得y1、y2的大小关系.
解答 解:(1)由y=x2-2x-3=(x-1)2-4可知顶点坐标为(1,-4),
令x=0,则y=-3,
∴与y轴交点为(0,-3),
令y=0,则0=x2-2x-3,解得x1=-1,x2=3,
∴与x轴交点为(-1,0),(3,0).
列表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y=x2-2x-3 | … | 0 | -3 | -4 | -3 | 0 | … |
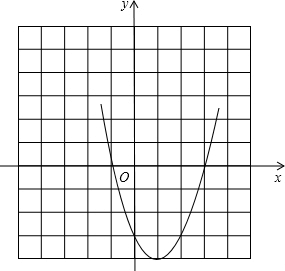
点评 本题考查了二次函数的图象,二次函数的性质,二次函数图象上点的坐标特征,找到顶点及对称轴,根据对称轴取点是画图的关键一步.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
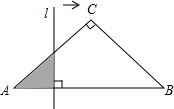 如图,在△ABC中,AC=BC,∠C=90°,直线l⊥AB,直线l从点A开始向右作匀速平行移动,设直线l移动的时间为t,扫过△ABC的面积(图中阴影部分)为S,则下列各图中,能够反映S关于t的函数关系的大致图象是( )
如图,在△ABC中,AC=BC,∠C=90°,直线l⊥AB,直线l从点A开始向右作匀速平行移动,设直线l移动的时间为t,扫过△ABC的面积(图中阴影部分)为S,则下列各图中,能够反映S关于t的函数关系的大致图象是( )| A. | 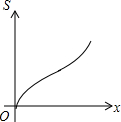 | B. | 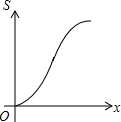 | C. | 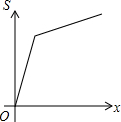 | D. | 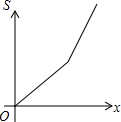 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
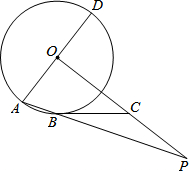 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
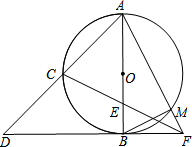 如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.
如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
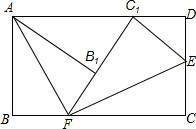 已知四边形ABCD是矩形,BF=1,FC=3,沿EF,AF折叠,点C落在C1处,点B落在FC1边上的B1,求AB=$\sqrt{5}$.
已知四边形ABCD是矩形,BF=1,FC=3,沿EF,AF折叠,点C落在C1处,点B落在FC1边上的B1,求AB=$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
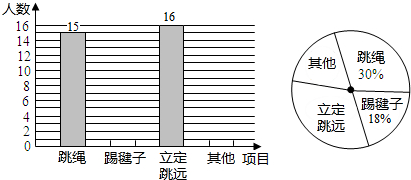
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com