Question

11．已知抛物线L：y=ax²+bx+c（b²-4ac＞0c≠0）分别交x轴于点A、B，交y轴于点C，则称△ABC为抛物线L的内接三角形，抛物线L称为△ABC的外接抛物线．
（1）如图①，抛物线y=-x²-3x+4的内接△ABC，求△ABC的面积．
（2）若抛物L的内接△ABC的面积为10，且A（-4，0），B（1，0），C（0，c），求抛物线L的解析式．
（3）如图②，若抛物L：y=-2x²-4x+c（c＞0）上有一点P（点P可以和点C 重合），且S_△PAB=mS_△ABC，请直接写出当c，m满足什么关系时，使得这样的点P的个数为2个．

Answer 1

分析 （1）令y=0可求得x₁=-4，x₂=1，故此可知AB=5，令x=0，得y=4从而得到点C的坐标为（0，4），故此可知OC=4，最后由三角形的面积公式可求得△ABC的面积；
（2）由题意可知；BA=5，由三角形的面积公式可知OC=4，当c=4时，抛物线的解析式为y=-x²-3x+4，当c=-4可求得抛物线的解析式为y=x²+3x-4；
（3）由抛物线的解析式可求得抛物线的对称轴方程为x=-1，将x=-1代入得y=2+c，从而得到抛物线的顶点坐标为（-1，2+c），在x轴的下方必然存在2个点P使得S_△PAB=mS_△ABC，故此再x轴的上S_△PAB＜mS_△ABC，从而得到PD＜mOC，故此可求得m与c的函数关系式．

解答 解：（1）∵令y=0得：-x²-3x+4=0，解得：x₁=-4，x₂=1，
∴AB=5．
∵令x=0，得y=4，
∴点C的坐标为（0，4）．
∴OC=4．
由三角形的面积公式可知：△ABC的面积=$\frac{1}{2}AB•OC$-$\frac{1}{2}×5×4$=10．
（2）∵A（-4，0），B（1，0），C（0，c），
∴AB=5，OC=|c|．
∵△ABC的面积为10，
∴$\frac{1}{2}AB×OC$=10，即$\frac{1}{2}×5×|c|=10$．
解得：|c|=4．
∴c=4或c=-4．
当c=4时，由（1）可知抛物线的解析式为y=-x²-3x+4．
当c=-4时，设抛物线的解析式为y=a（x+4）（x-1），
∵将点（0，-4）代入得；a=1．
∴抛物线的解析式为y=x²+3x-4．
∴抛物线的解析式为y=-x²-3x+4或y=x²+3x-4．
（3）如图所示：当点P为与抛物线的顶点时，过点P作PD⊥x轴，垂足为D．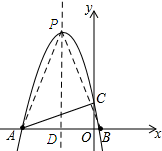

由x=-$\frac{b}{2a}$可知抛物线的对称轴方程为x=$-\frac{-4}{-2×2}$=-1．
∵将x=-1代入抛物线的解析式得y=2+c．
∴PD=2+c．
∴抛物线的顶点坐标为（-1，2+c）．
令x=0得，y=c．
∴OC=c．
∵使得S_△PAB=mS_△ABC的点P的个数为2个，
∴当点P为抛物线的顶点时，S_△PAB＜mS_△ABC．
∴PD＜mOC，即2+c＜mc．
整理得：c（m-1）＞2．
∴c，m的关系式为c（m-1）＞2．

点评 本题主要考查的是二次函数的综合应用，应用了待定系数法求二次函数的解析式、二次函数的图象和性质、三角形的面积公式，明确当点P为抛物线的顶点且S_△PAB＜mS_△ABC时抛物线上存在2个点P使得S_△PAB=mS_△ABC是解题的关键．