练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．计算：$\sqrt{12}$-4$\sqrt{\frac{1}{2}}$-tan60°+|$\sqrt{3}$-2|．

    分析 原式前两项化为最简二次根式，第三项利用特殊角的三角函数值计算，最后一项利用绝对值的代数意义化简，计算即可得到结果．

    解答 解：原式=2$\sqrt{3}$-4×$\frac{\sqrt{2}}{2}$-$\sqrt{3}$+2-$\sqrt{3}$
    =2-2$\sqrt{2}$．

    点评 此题考查了实数的运算，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

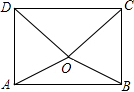    10．如图，O为矩形ABCD内的一点，满足OD=OC，若O点到边AB的距离为d，到边DC的距离为3d，且OB=2d，求该矩形对角线的长2$\sqrt{7}$d．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．已知数的大小比较：①-1＞0；②-1＜0；③-1＞-2；④-1＜-2．其中正确的有（　　）
    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．小亮做了一个用于放试管的木架子，他在$\frac{83}{4}$厘米长的木条上钻了7个孔，每个孔的直径都为a厘米，如图所示：

    （1）如果两端的空间与任何相邻两孔之间的距离相同，当a=$\frac{5}{4}$时，请计算相邻两孔之间的距离是多少厘米？
    （2）如果两端的空间都是$\frac{3}{2}$，其它相邻两孔之间的距离相同都为$\frac{43}{24}$，请计算每个孔的直径为多少厘米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．甲车和乙车从A、B两地同时出发，沿同一线路相向匀速行驶，出发后1.5h两车相遇，相遇时甲车比乙车少走30km，相遇后1.2h乙车到达A地．
    （1）两车的行驶速度分别是多少？
    （2）相遇后，若乙车速度不变，甲车想和乙车同时到达目的地，那么甲车要比原来的行驶速度增加多少km/h？
    （3）相遇后，甲车到B地间的部分路段限速120km/h，部分路段限速140km/h，（2）中甲车在相应路段，既不超速又不低于限速行驶，刚好能和乙车同时到达目的地，试求限速120km/h和限速140km/h的路段各多少km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

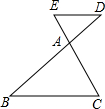    5．如图，已知点D、E分别在△ABC的边BA、CA的延长上，下列给出的条件中，不能判定DE∥BC的是（　　）
    A．BD：AB=CE：ACB．DE：BC=AB：ADC．AB：AC=AD：AED．AD：DB=AE：EC

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，梯形ABCD中，AD∥BC，∠A=90°，AD=4，AB=8，BC=10，M在边CD上，且$\frac{DM}{MC}=\frac{2}{3}$．
    （1）如图①，联结BM，求证：BM⊥DC；
    （2）如图②，作∠EMF=90°，ME交射线AB于点E，MF交射线BC于点F，若AE=x，BF=y． 当点F在线段BC上时，求y关于x的函数解析式，并写出定义域；
    （3）若△MCF是等腰三角形，求AE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

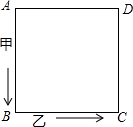    9．如图，两人沿着边长为70米的正方形，按A→B→C→D→A…的方向行走．甲从A点以65米/分的速度、乙从B点以72米/分的速度行走，甲、乙两人同时出发，当乙第一次追上甲时，将在正方形的AD边上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．等边△ABC高为7$\sqrt{3}$，边长为14．BD为AC边上高，P是BD上的动点，且E是BC上-点，BE=CE，则△PEC的周长最小值为7$\sqrt{3}$+7．

    查看答案和解析>>

    同步练习册答案