Question

12．如图，梯形ABCD中，AD∥BC，∠A=90°，AD=4，AB=8，BC=10，M在边CD上，且$\frac{DM}{MC}=\frac{2}{3}$．
（1）如图①，联结BM，求证：BM⊥DC；
（2）如图②，作∠EMF=90°，ME交射线AB于点E，MF交射线BC于点F，若AE=x，BF=y． 当点F在线段BC上时，求y关于x的函数解析式，并写出定义域；
（3）若△MCF是等腰三角形，求AE的值．

Answer 1

分析 （1）连接BD，作DN⊥BC于N，则四边形ABND是矩形，得出DN=AB=8，BN=AD=4，求出CN=BC-BN=6，由勾股定理求出CD，得出CD=BC=10，由等腰三角形的性质和平行线的性质得出∠ADB=∠DBC=∠BDC，求出DM=4=AD，由SAS证明△ADB≌△MDB，得出对应角相等即可；
（2）由角的互余关系得出∠C=∠MBA，∠CMF=∠BME，证出△CMF∽△BME，得出对应边成比例，即可得出结果；
（3）分两种情况：①当点E在线段AB上时，△CMF∽△BME，△CMF为等腰三角形，得出△BME为等腰三角形，当BE=BM=8时，AE=0；当BM=ME时，由三角函数求出BE=$\frac{48}{5}$＞AE，舍去；当BE=ME时，由三角函数求出BE=$\frac{20}{3}$，得出AE=AB-BE=$\frac{4}{3}$；
②当点E在BC延长线上时，同（2）可证△CMF∽△BME，△BME为等腰三角形，由∠MBE＞90°，得出BE=BM=8，因此AE=16；即可得出结果．

解答 （1）证明：连接BD，如图1所示：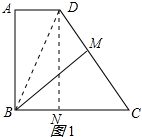
作DN⊥BC于N，则∠DNC=90°，四边形ABND是矩形，
∴DN=AB=8，BN=AD=4，
∴CN=BC-BN=10-4=6，
CD=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∴CD=BC=10，
∴∠DBC=∠BDC，
∵AD∥BC，
∴∠ADB=∠DBC=∠BDC，
∵$\frac{DM}{MC}=\frac{2}{3}$，
∴DM=4=AD，
在△ADB和△MDB中，
$\left\{\begin{array}{l}{AD=DM}&{\;}\\{∠ADB=∠BDC}&{\;}\\{BD=BD}&{\;}\end{array}\right.$，
∴△ADB≌△MDB（SAS），
∴∠DMB=∠A=90°，
BM=AB=8，
∴BM⊥DC；
（2）解：∵∠C=∠MBA=90°-∠MBC，
∠CMF=∠BME=90°-∠FMB，
∴△CMF∽△BME，
∴$\frac{CF}{BE}=\frac{CM}{BM}$，
即$\frac{10-y}{8-x}=\frac{6}{8}$，
解得：y=$\frac{3}{4}$x+4（0≤x≤8）；
（3）解：分两种情况：
①当点E在线段AB上时，△CMF∽△BME，△CMF为等腰三角形，
∴△BME为等腰三角形，
当BE=BM=8时，AE=0；
当BM=ME时，BE=2×BM×cos∠MBA=2×8×$\frac{3}{5}$=$\frac{48}{5}$＞AE，舍去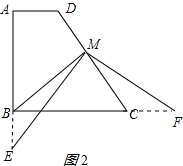
当BE=ME时，BE=$\frac{\frac{1}{2}BM}{cos∠MBA}$=$\frac{\frac{1}{2}×8}{\frac{3}{5}}$=$\frac{20}{3}$，
∴AE=AB-BE=8-$\frac{20}{3}$=$\frac{4}{3}$；
②当点E在BC延长线上时，如图2所示：
同（2）可证△CMF∽△BME，△BME为等腰三角形，
又∵∠MBE＞90°，
∴BE=BM=8，
∴AE=16．
综上所述：若△MCF是等腰三角形，AE的值为0或$\frac{4}{3}$或16．

点评 本题是四边形综合题目，考查了梯形的性质、相似三角形的判定与性质、全等三角形的判定与性质、矩形的判定与性质、等腰三角形的判定与性质、三角函数等知识；本题综合性强，难度较大，特别是（3）中，需要进行分类讨论才能得出结果．