
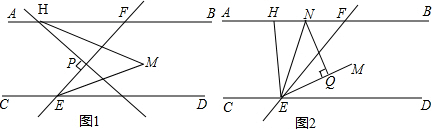
分析 (1)首先作MQ∥AB,根据平行线的性质,推得∠M=$\frac{1}{2}$(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(2)①首先判断出∠NEQ=∠NEF+∠QEF=$\frac{1}{2}$(∠HEF+∠DEF)=$\frac{1}{2}$∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=$\frac{1}{2}$(180°-∠HED)=$\frac{1}{2}$∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
②首先判断出∠NEQ=∠QEF-∠NEF=$\frac{1}{2}$(∠DEF-∠HEF)=$\frac{1}{2}$∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=$\frac{1}{2}$(180°-∠HED)=$\frac{1}{2}$∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
解答 解:(1)如图1,作MQ∥AB,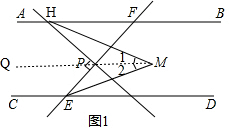 ,
,
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=$\frac{1}{2}$(∠FHP+∠FED)=$\frac{1}{2}$(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°-90°=90°,
∵∠1+∠2=∠M,
∴∠M=$\frac{1}{2}×90°=45°$.
(2)①如图2,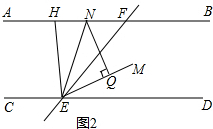 ,
,
∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=$\frac{1}{2}$(∠HEF+∠DEF)=$\frac{1}{2}$∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=$\frac{1}{2}$(180°-∠HED)=$\frac{1}{2}$∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3, ,
,
∠FHE=180°-2∠ENQ,理由如下:
∠NEQ=∠QEF-∠NEF=$\frac{1}{2}$(∠DEF-∠HEF)=$\frac{1}{2}$∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=$\frac{1}{2}$(180°-∠HED)=$\frac{1}{2}$∠CEH,
∵AB∥CD,
∴∠FHE=180°-∠CEH=180°-2∠ENQ.
综上,可得
当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°-2∠ENQ.
点评 此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
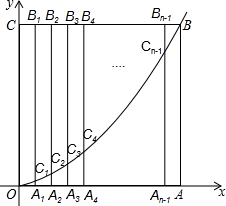 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,当B25C25=8C25A25时,则n=75.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,当B25C25=8C25A25时,则n=75.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 顺次连接矩形各边中点的四边形一定也是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 有一个角是直角的菱形一定是正方形 | |
| D. | 平行四边形的对角线相等且互相平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}x+y=21\\ 5x=2y\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}x+y=21\\ 2x=5y\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}2x+5y=21\\ 2x=5y\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}2x+5y=21\\ 5x=2y\end{array}}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com