
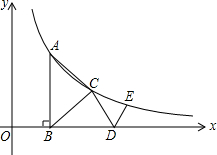
 如图,△ABC是等腰直角三角形,斜边AD⊥x轴于D,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴的正半轴上,则点E的坐标是($\sqrt{3}$+1,$\sqrt{3}$-1).
如图,△ABC是等腰直角三角形,斜边AD⊥x轴于D,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴的正半轴上,则点E的坐标是($\sqrt{3}$+1,$\sqrt{3}$-1). 分析 作EH⊥x轴于H,作CF∥x轴交AB于F,交EH于Q,如图,根据等腰直角三角形的性质得CF⊥AB,AF=CF,设A(t,$\frac{2}{t}$),则AF=CF=$\frac{1}{t}$,得到C(t+$\frac{1}{t}$,$\frac{1}{t}$),利用反比例函数图象上点的坐标特征得t+$\frac{1}{t}$)•$\frac{1}{t}$=2,解得t1=1,t2=-1(舍去),所以C(2,1),接着证明△CEQ≌△EDH得到CQ=EH,设E(a,$\frac{2}{a}$),则EH=$\frac{2}{a}$,Q(a,1),CQ=a-2,所以a-2=$\frac{2}{a}$,然后解方程求出a的值即可得到E点坐标.
解答 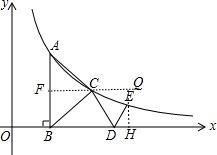 解:作EH⊥x轴于H,作CF∥x轴交AB于F,交EH于Q,如图,
解:作EH⊥x轴于H,作CF∥x轴交AB于F,交EH于Q,如图,
∵△ABC是等腰直角三角形,斜边AB⊥x轴于B,
∴CF⊥AB,AF=CF,
设A(t,$\frac{2}{t}$),则AF=CF=$\frac{1}{t}$,
∴C(t+$\frac{1}{t}$,$\frac{1}{t}$),
∵C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,
∴t+$\frac{1}{t}$)•$\frac{1}{t}$=2,解得t1=1,t2=-1(舍去),
∴C(2,1),
∵△CDE为等腰直角三角形,
∴EC=ED,∠CED=90°,
∴∠CEQ+∠DEH=90°,
而∠CEQ+∠ECQ=90°,
∴∠DEH=∠ECQ,
在△CEQ和△EDH中
$\left\{\begin{array}{l}{∠CQE=∠EHD}\\{∠ECQ=∠DEH}\\{CE=ED}\end{array}\right.$,
∴△CEQ≌△EDH,
∴CQ=EH,
设E(a,$\frac{2}{a}$),则EH=$\frac{2}{a}$,Q(a,1),
∴CQ=a-2,
∴a-2=$\frac{2}{a}$,
整理得a2-2a-2=0,解得a1=$\sqrt{3}$+1,a2=-$\sqrt{3}$+1(舍去),
∴E点坐标为($\sqrt{3}$+1,$\sqrt{3}$-1).
故答案为($\sqrt{3}$+1,$\sqrt{3}$-1).
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了等腰直角三角形.


科目:初中数学 来源: 题型:解答题
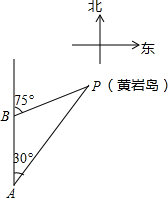 如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)
如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.
如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
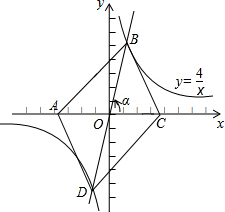 如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)
如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种货车 | 乙种货车 | |
| 载货量(吨/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com