
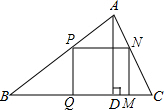
 如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.
如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽. 分析 根据矩形性质得PN∥BC,PQ=DE,则可证明△APN∽△ABC,根据相似的性质得$\frac{PN}{BC}$=$\frac{AE}{AD}$,设PQ=x,则ED=x,AE=AD-DE=8-x,然后分类讨论:当PN=2PQ时,即PN=2x,则$\frac{2x}{12}$=$\frac{8-x}{8}$;当PN=$\frac{1}{2}$PQ时,即PN=$\frac{1}{2}$x,则$\frac{\frac{1}{2}x}{12}$=$\frac{8-x}{8}$,再分别解方程求出x,从而可得到矩形的长与宽.
解答 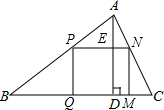 解:如图,
解:如图,
∵四边形PQMN为矩形,
∴PN∥BC,PQ=DE,
∴△APN∽△ABC,
∴$\frac{PN}{BC}$=$\frac{AE}{AD}$,
设PQ=x,则ED=x,AE=AD-DE=8-x,
当PN=2PQ时,即PN=2x,则$\frac{2x}{12}$=$\frac{8-x}{8}$,解得x=$\frac{24}{7}$,所以2x=$\frac{48}{7}$,此时矩形的长、宽分别为$\frac{48}{7}$,$\frac{24}{7}$;
当PN=$\frac{1}{2}$PQ时,即PN=$\frac{1}{2}$x,则$\frac{\frac{1}{2}x}{12}$=$\frac{8-x}{8}$,解得x=6,所以$\frac{1}{2}$x=3,此时矩形的长、宽分别为6,3;
所以矩形的长、宽分别为$\frac{48}{7}$cm,$\frac{24}{7}$cm或6cm,3cm.
点评 本题考查了相似三角形的应用:在实际问题中抽象出几何图形,通过证明三角形相似,利用相似比表示线段之间的关系和计算线段的长.


科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b≤0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
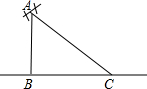 如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )
如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )| A. | 6米 | B. | 7米 | C. | 8米 | D. | 9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5{x}^{2}}$ | B. | $\sqrt{0.9}$ | C. | $\sqrt{\frac{3}{7}}$ | D. | $\sqrt{{a}^{2}-3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com