
| A. | $\sqrt{5{x}^{2}}$ | B. | $\sqrt{0.9}$ | C. | $\sqrt{\frac{3}{7}}$ | D. | $\sqrt{{a}^{2}-3}$ |
科目:初中数学 来源: 题型:解答题
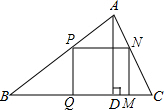 如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.
如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
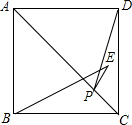 如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
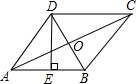 如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )
如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )| A. | ①②④⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ①②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 生产A种型号零件/件 | 生产B种型号零件/件 | 总时间/分 |
| 2 | 2 | 70 |
| 6 | 4 | 170 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com