
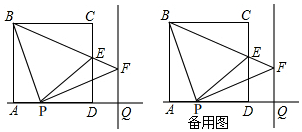
���� ��1�����жϳ�AB=PQ����ͬ�ǵ������ȵó���ABP=��QPF�������ó���BAP�ա�PQF�������жϳ�������BPF�ǵ���ֱ�������μ��ɣ�
��2���������������������ȫ�ȡ���ƽ���߶��������˶����ص㼴���жϳ����ۣ�
��3�����жϳ�DGFQ�DZ߳�Ϊ1�������Σ��������������ε����ʵó�EG�������ó�DE������ù��ɶ�������������ۣ�
��� �⣺��1�����˶�֪��AP=DQ��
��PQ=PD+DQ=PD+AP=AD��
���ı���ABCD�������Σ�
��AB=AD��
��AB=PQ��
��FQ��AD��
���PQF=��BAD=90�㣬
���APB+��ABP=90�㣬
��AP��PF��
���APB+��FPQ=90�㣬
���ABP=��QPF��
�ڡ�BAP�͡�PQF�У�$\left\{\begin{array}{l}{��ABP=��QPF}\\{AB=PQ}\\{��BAP=��PQF}\end{array}\right.$��
���BAP�ա�PQF��
��PB=PF��AP=FQ=t��
���BPF�ǵ���ֱ�������Σ�
���PBF=45�㣬
��2����ͼ��
����BD��
��BP=BEʱ��
��Rt��ABP��Rt��CBE��$\left\{\begin{array}{l}{BP=BE}\\{AB=BC}\end{array}\right.$��
��Rt��ABP��Rt��CBE��
���ABP=��CBE��
�ߡ�ABP+��CBE=45�㣬
���ABP=22.5�㣬
�ߡ�ABD=45�㣬
���DBPP=22.5��=��ABP��
��AP�ǡ�BAC��ƽ���ߣ�
��$\frac{AB}{BD}=\frac{AP}{DP}$
��BD=$\sqrt{2}$AB��AP=t��PD=AD-AP=6-t��
��$\frac{AB}{\sqrt{2}AB}=\frac{t}{6-t}$��
��t=6��$\sqrt{2}$-1����
��PB=PEʱ���ɣ�1��֪��PB=PF��
���F��E�غϣ�
������E��F��D�غϣ���P��A�غϣ�
��ʱ��t=0��
��EB=EPʱ����BPE=��EBP=45�㣬
���BEP=90�㣬
���F�͵�D�غϣ�
��ʱ����P�͵�D�غϣ�
��AP=AD=6��
��t=6��1=6��
��������PBEΪ����������ʱ��t��ֵΪ0��6��$\sqrt{2}$-1����6��
��3����ͼ1�� ����F��FG��CD��
����F��FG��CD��
���DGF=90�㣬
�ߡ�GDQ=��FQD=90�㣬
���ı���DGFQ�Ǿ��Σ�
���˶�֪��AP=DQ=FQ=1��
�����DGFQ�DZ߳�Ϊ1�������Σ�
��DG=1��
��CG=CD-DG=5��
��BC��FG��
���BCE�ס�FGE��
��$\frac{BC}{FG}=\frac{CE}{GE}$��
��$\frac{CE}{GE}=\frac{6}{1}$��
��EG=$\frac{1}{7}$CG=$\frac{5}{7}$��
��DE=DG+EG=1+$\frac{5}{7}$=$\frac{12}{7}$��
��Rt��EDP��DP=AD-AP=5��
��PE=$\sqrt{D{P}^{2}+D{E}^{2}}$=$\frac{37}{7}$��
���� �������ı����ۺ��⣬��Ҫ������ȫ�������ε����ʺ��ж�����ƽ���߶��������ε��ж������ʣ������ε��ж������ʣ����������ε��ж������ʣ��Ȿ��Ĺؼ����жϳ���PBF=45�㣬��һ���е��Ѷȵ��п������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 75�� | C�� | 105�� | D�� | 120�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪���ڡ�ABC�У���B=60�㣬��BAC=70�㣬AD��BC��D����CAD=40�㣮
��ͼ����֪���ڡ�ABC�У���B=60�㣬��BAC=70�㣬AD��BC��D����CAD=40�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�D��BC�ߵ��е㣬ADƽ�֡�BAC��DE��AB��E��DF��AC��F����֤����B=��C��
��ͼ����ABC�У�D��BC�ߵ��е㣬ADƽ�֡�BAC��DE��AB��E��DF��AC��F����֤����B=��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
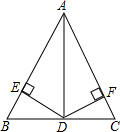 ��֪����ͼ����ABC�У�ADƽ�֡�BAC����BD=CD��DE��AB��DF��AC������ֱ�ΪE��F����֤��EB=FC��
��֪����ͼ����ABC�У�ADƽ�֡�BAC����BD=CD��DE��AB��DF��AC������ֱ�ΪE��F����֤��EB=FC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 +3��x-1��=x2-5x+1
+3��x-1��=x2-5x+1�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD��BEFG��Ϊ�����Σ�
��ͼ���ı���ABCD��BEFG��Ϊ�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com