
分析 根据比赛场数乘以每场的得分,可得总得分,根据其他队的得分与两队得分的和也是总得分,可得方程,根据队数、得分数都是整数,可得答案.
解答 解:设参加此次比赛的足球队共有x支(x为正奇数),则全部比赛场次为$\frac{1}{2}$x(x-1),
∵每场得一分,
∴共得$\frac{1}{2}$x(x-1)分,
设其他队的平均分为y,(y为正整数),则总得分为10+y(x-2)
∴根据题意得,$\frac{1}{2}$x(x-1)=10+y(x-2),
∴y=$\frac{{x}^{2}-x-20}{2(x-2)}$=$\frac{{(x}^{2}-x-2)-18}{2(x-2)}$=$\frac{(x+1)(x-2)-18}{2(x-2)}$=$\frac{x+1}{2}$-$\frac{9}{x-2}$,
∵x为正奇数,
∴$\frac{x+1}{2}$为正整数,
∵y为正整数,
∴$\frac{9}{x-2}$是正整数,
∴(x-2)必须是9的因数,9的因数有1、3、9,
∴(x-2)可能为1、3、9,
∴x=3、5、11.
∵其中有两队共得10分,
∴$\frac{1}{2}$x(x-1)>10,
∴x2-x-20>0,
∴(x+4)(x-5)>0,
∴x>5或x<-4(舍),
∴x=11,
所以参加此次比赛的足球队共有11支.
点评 此题是应用类问题,主要考查了列方程,整数解,解一元二次不等式,因数,倍数,解本题的关键是根据题意列出方程,用x表示y之后处理成$\frac{x+1}{2}$-$\frac{9}{x-2}$是解本题的难点.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{m}$ | B. | $\sqrt{-m}$ | C. | -$\sqrt{m}$ | D. | -$\sqrt{-m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
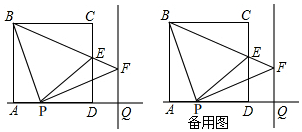
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
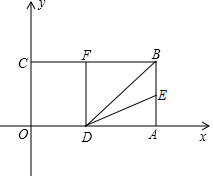 如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处.
如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:
如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com