
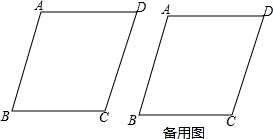
分析 (1)连接BD、AC交于点O,作AH⊥BC于H,由菱形的性质得出AO=OC=3,BO=4,由△ABC的面积求出AH=$\frac{24}{5}$,由勾股定理得出BH,即可得出结果;
(2)由菱形的性质得出∠FAC=∠ACB,证出△ABC∽△ECF,得出对应边成比例$\frac{AB}{CE}$=$\frac{AC}{EF}$,求出EF,由平行线得出△MBC∽△MAF,得出$\frac{BM}{AM}$=$\frac{BC}{AF}$=$\frac{25}{36}$,即可得出结果;
(3)作EM⊥BC于M,作EG∥BC交CF于G,由(1)知cos∠B=$\frac{7}{25}$,BE=x,得出BM=$\frac{7}{25}$x,由勾股定理得出EM=$\frac{24}{25}$x,CE=$\sqrt{E{M}^{2}+M{C}^{2}}$=$\sqrt{{x}^{2}-\frac{14}{5}x+25}$,由平行线得出∠GEC=∠ECB,$\frac{BC}{EG}=\frac{BM}{ME}$,证出△BCE∽△CEG,得出对应边成比例$\frac{BC}{CE}=\frac{CE}{EG}$,得出EG=$\frac{C{E}^{2}}{BC}$=$\frac{5{x}^{2}-14x+125}{25}$,代入比例式即可得出y关于x的函数解析式为y=$\frac{125}{5x-14}$($\frac{14}{5}$<x≤5).
解答 解:(1)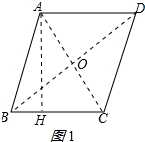 连接BD、AC交于点O,作AH⊥BC于H,如图1所示:
连接BD、AC交于点O,作AH⊥BC于H,如图1所示:
则AO=OC=3,BO=4,
∵S△ABC=$\frac{1}{2}$BC×AH=$\frac{1}{2}$AC×BO=$\frac{1}{2}$×6×4=12,
∴$\frac{1}{2}$×5×AH=12,
解得:AH=$\frac{24}{5}$,
由勾股定理得:BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{5}^{2}-(\frac{24}{5})^{2}}$=$\frac{7}{5}$,
∴cos∠B=$\frac{BH}{AB}$=$\frac{\frac{7}{5}}{5}$=$\frac{7}{25}$;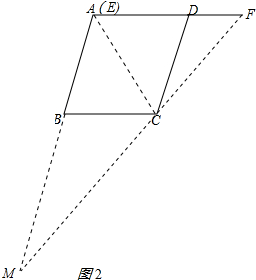
(2)当点E与点A重合时,符合题意的图形,如图2所示:
∵四边形ABCD为菱形,
∴∠FAC=∠ACB,
∵∠ECF=∠B,
∴△ABC∽△ECF,
∴$\frac{AB}{CE}$=$\frac{AC}{EF}$,即$\frac{5}{6}$=$\frac{6}{EF}$,
解得:EF=$\frac{36}{5}$,
∵BC∥AF,
∴△MBC∽△MAF,
∴$\frac{BM}{AM}$=$\frac{BC}{AF}$=$\frac{5}{\frac{36}{5}}$=$\frac{25}{36}$,
∴$\frac{BM}{BM+5}$=$\frac{25}{36}$,
解得:BM=$\frac{125}{11}$;
(3)作EH⊥BC于H,作EG∥BC交CF于G,如图3所示: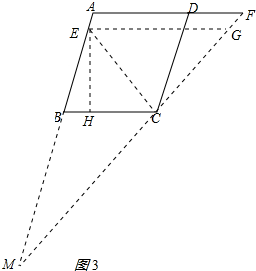
由(1)知cos∠B=$\frac{7}{25}$,BE=x,
∴BH=$\frac{7}{25}$x,EH=$\sqrt{B{E}^{2}-B{H}^{2}}$=$\sqrt{{x}^{2}-(\frac{7}{25}x)^{2}}$=$\frac{24}{25}$x,
∴CE=$\sqrt{E{H}^{2}+C{H}^{2}}$=$\sqrt{(5-\frac{7}{25}x)^{2}+(\frac{24}{25}x)^{2}}$=$\sqrt{{x}^{2}-\frac{14}{5}x+25}$,
∵EG∥BC,
∴∠GEC=∠ECB,$\frac{BC}{EG}=\frac{BM}{ME}$,
∴△BCE∽△CEG,
∴$\frac{BC}{CE}=\frac{CE}{EG}$,
则EG=$\frac{C{E}^{2}}{BC}$=$\frac{5{x}^{2}-14x+125}{25}$,
∴$\frac{5}{\frac{5{x}^{2}-14x+125}{25}}=\frac{y}{x+y}$,
整理得:y=$\frac{125}{5x-14}$,
即y关于x的函数解析式为y=$\frac{125}{5x-14}$($\frac{14}{5}$<x≤5).
点评 本题是相似形综合题目,考查了菱形的性质、相似三角形的判定与性质、平行线的性质、勾股定理、三角函数等知识;本题综合性强,难度较大,特别是(3)中,需要运用勾股定理和证明三角形相似得出比例式才能得出结果.


科目:初中数学 来源: 题型:填空题
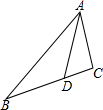 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任意打开一本200页的数学书,恰好是第50页 | |
| B. | 打开电视机,任选一个频道,正在播放足球赛 | |
| C. | 在空旷的操场上向上抛出的篮球一定会下落 | |
| D. | 阴天一定会下雨 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13道 | B. | 14道 | C. | 15道 | D. | 16道 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com