练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．将18.25°换算成度、分、秒的结果是18°15′0″．

    分析 根据大单位化小单位乘以进率，可得答案．

    解答 解：18.25°=18°+0.25×60=18°15′0″，
    故答案为：18°15′0″．

    点评 本题考查了度分秒的换算，利用大单位化小单位乘以进率是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．下列命题是假命题的是（　　）
    A．如果a∥b，b∥c，那么a∥c
    B．直角三角形的两个锐角互余
    C．两条直线被第三条直线所截，内错角相等
    D．两点之间，线段最短

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解方程：
    （1）3x-2=3+2x
    （2）$\frac{3+x}{2}-1=\frac{x+2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．整式-0.3x2y，0，$\frac{x+1}{2}$，$\frac{1}{a}$，$\frac{1}{3}$x2，-$\frac{1}{4}$y，-$\frac{1}{3}$ab2+$\frac{1}{2}$中，单项式的个数有（　　）
    A．3个B．4个C．5个D．6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

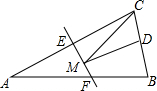    9．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（　　）
    A．6B．8C．10D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

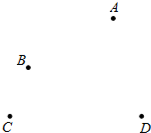    19．如图，平面上四个点A，B，C，D．按要求完成下列问题：
    （1）连接AD；
    （2）画射线AB，联结DC并延长与射线AB交于点E；
    （3）用量角器作∠BAD的平分线AF，AF与CD交于点F；
    （4）过点B作BH⊥CD于点H，并用刻度尺度量得BH的长度为1.3cm（精确到0.1cm）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列方程变形中，正确的是（　　）
    A．方程3x-2=2x+1，移项，得3x-2x=-1+2
    B．方程3-x=2-5（x-1），去括号，得3-x=2-5x-1
    C．方程$\frac{2}{3}$t=$\frac{3}{2}$，系数化为1，得t=1
    D．方程$\frac{x-1}{2}$=$\frac{x}{5}$，去分母，得5（x-1）=2x

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知点A（a-2b，-2）与点A′（-6，2a+b）关于坐标原点对称，则3a-b=8．

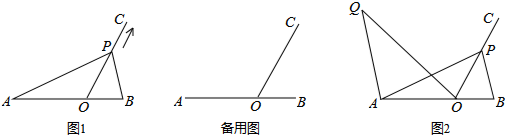
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，点O在线段AB上，AO=2，OB=1，OC为射线，且∠BOC=60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．

    （1）当t=$\frac{1}{2}$秒时，则OP=1，S△ABP=$\frac{3\sqrt{3}}{4}$；
    （2）当△ABP是直角三角形时，求t的值；
    （3）如图2，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求证：AQ•BP=3．为了证明AQ•BP=3，小华同学尝试过O点作OE∥AP交BP于点E．试利用小华同学给我们的启发补全图形并证明AQ•BP=3．

    查看答案和解析>>

    同步练习册答案