练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．已知有理数x，y，z满足条件：|x-z-2|+|3x-6y-7|+（3y+3z-4）2=0，则xyz=1．

    分析 已知等式为三个非负数的和为0的形式，只有这几个非负数都为0，可组成方程组，求x、y、z的值，即可求得xyz的值．

    解答 解：根据非负数的性质，得$\left\{\begin{array}{l}{x-z-2=0①}\\{3x-6y-7=0②}\\{3y+3z-4=0③}\end{array}\right.$
    ①×3-②，得6y-3z+1=0④
    ④+③，得9y=3，
    解得y=$\frac{1}{3}$，
    把y=$\frac{1}{3}$代入④得z=1，
    把z=1代入①得x=3．
    ∴xyz=3×$\frac{1}{3}$×1=1．
    故答案为1．

    点评 考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0，三元一次方程组的解法，代数式求值，综合题，难度较大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．已知x=2是关于x的一元一次方程mx+2=0的解，则m的值为（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．画出如图所示物体的主视图、左视图、俯视图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知抛物线的顶点A的坐标为（4，6），且经过点B（0，2）．
    （1）求此抛物线的解析式；
    （2）若点P在直线y=x上，且PA+PB的值最小，求点P的坐标及PA+PB的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）（-1）2013-|-2|+（$\sqrt{3}-π$）0×$\root{3}{8}$-（$\frac{1}{4}$）-1．
    （2）|-2|+（3-π）0-2-1+$\root{3}{-27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知a、b满足a+b+4=4$\sqrt{a-2}$+2$\sqrt{b+1}$，判断$\frac{a}{b}$值的情况．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．一次函数y=kx+b（k≠0）的图象与x轴的交点的横坐标是方程kx+b=0的解．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年河南省七年级下学期第一次月考（3月）数学试卷（解析版） 题型：填空题

    如图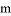，∥，∠1＝120°，∠A＝55°，则∠ACB的大小是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（　　）
    A．34°B．56°C．66°D．54°

    查看答案和解析>>

    同步练习册答案