
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上运动(不与点
上运动(不与点![]() ,
,![]() 重合),以
重合),以![]() 为边作正方形
为边作正方形![]() ,使点
,使点![]() 在正方形
在正方形![]() 内,连接
内,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②当
;②当![]() 时,
时,![]() ;③点
;③点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;④
;④![]() 面积的最大值是
面积的最大值是![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)

【答案】②③④
【解析】
过点F作FH⊥AB于点H,过点E作EG⊥CA延长线于点G,根据题意可得在△BCD与△ECD中有BD=ED,CD=CD,但无法得到BC=EC或∠EDC=∠BDC,故△BCD与△ECD不一定全等,故①错误;先推出∠ACB=30°,再由此得出AC=![]() a,再根据CD=2AD,即可得出tan∠ADB=
a,再根据CD=2AD,即可得出tan∠ADB=![]() ,可得∠ADB=60°,由此即可得出∠ADE=30°,故②正确;先证明△FHB≌△BAD,根据全等三角形的性质可得FH=a,故③正确;先证明△EGD≌△DAB,设CD=x,
,可得∠ADB=60°,由此即可得出∠ADE=30°,故②正确;先证明△FHB≌△BAD,根据全等三角形的性质可得FH=a,故③正确;先证明△EGD≌△DAB,设CD=x,
用含x的代数式表达S△CDE,再根据二次函数的性质可得△CDE面积最大值是![]() a2,故④正确.
a2,故④正确.
如图所示,
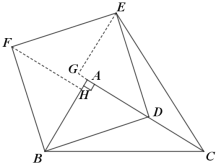
过点F作FH⊥AB于点H,过点E作EG⊥CA延长线于点G,
∵四边形BDEF为正方形,
∴BD=DE=EF=BF,∠FBD=∠BDE=∠BFE=90°,
在△BCD与△ECD中有BD=ED,CD=CD,而无法得到BC=EC或∠EDC=∠BDC,
∴△BCD与△ECD不一定全等,故①错误;
∵∠BAC=90°,AB=![]() BC=a,
BC=a,
sin∠ACB=![]() =
=![]() =
=![]() ,即∠ACB=30°,
,即∠ACB=30°,
tan∠ACB=tan30°=![]() =
=![]() =
=![]() ,
,
∴AC=![]() a,
a,
又CD=2AD,
∴AD=![]() (AD+CD)=
(AD+CD)=![]() AC=
AC=![]() a,
a,
∴tan∠ADB=![]() =
=![]() =
=![]() ,
,
∴∠ADB=60°,
又∠BDE=∠ADB+∠ADE=90°,
∴∠ADE=90°-∠ADB=90°-60°=30°,故②正确;
∵FH⊥AB,
∴∠FHB=90°,∠HFB+∠HBF=90°,
又∠FBD=∠HBF+∠ABD=90°,
∴∠ABD=∠HFB,
在△FHB与△BAD中有: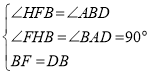 ,
,
∴△FHB≌△BAD(AAS),
∴FH=BA=a,
∴F到直线AB的距离为FH=a,故③正确;
∵EG⊥CA,
∠EGD=90°,
∴S△CDE=![]() CD×EG,
CD×EG,
∵∠BDE=∠ADB+∠GDE=90°,∠GED+∠GDE=90°,
∴∠GED=∠ADB,
在△EGD与△DAB中有: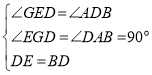 ,
,
∴△EGD≌△DAB(AAS),
∴EG=AD,
∴AC=AD+CD=EG+CD=![]() =
=![]() =
=![]() a,
a,
∴AD=EG=![]() a-CD,
a-CD,
设CD=x,则AD=EG=![]() a-x,
a-x,
S△CDE=![]() x(
x(![]() a-x)
a-x)
=![]() x2+
x2+![]() ax
ax
=![]() (x2-
(x2-![]() ax)
ax)
=![]() (x-
(x-![]() a)2+
a)2+![]() a2
a2
∴关于x的二次函数图象开口向下,
当x=CD=![]() a时S△CDE取最大值为
a时S△CDE取最大值为![]() a2,
a2,
∴△CDE面积最大值是![]() a2,故④正确;
a2,故④正确;
∴其中正确的结论是②③④,
故答案为:②③④.


科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的动点(与点
上的动点(与点![]() 、
、![]() 不重合),且
不重合),且![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
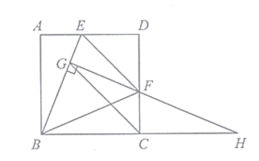
(1)求证:①![]()
![]()
![]() ;②
;②![]() ;
;
(2)若![]() ,在点
,在点![]() 运动过程中,探究:
运动过程中,探究:
①线段![]() 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
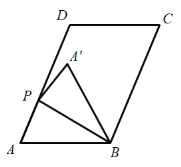
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为![]() 米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设
米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设![]() 的长度为
的长度为![]() 米,矩形区域
米,矩形区域![]() 的面积为
的面积为![]() 米
米![]() .
.
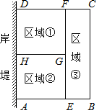
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,点C为圆上一点,将劣弧![]() 沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )

A.35°B.40°C.45°D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=4,C为半圆AB的中点,P为![]() 上一动点,延长BP至点Q,使BPBQ=AB2.若点P由A运动到C,则点Q运动的路径长为_____.
上一动点,延长BP至点Q,使BPBQ=AB2.若点P由A运动到C,则点Q运动的路径长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com