练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知（x2+y2）2+5（x2+y2）-6=0，则x2+y2的值为1．

    分析 先设x2+y2=t，则方程即可变形为t2+5t-6=0，解方程即可求得t即x2+y2的值．

    解答 解：设x2+y2=t，则原方程可化为：t2+5t-6=0
    即（t+6）（t-1）=0
    ∴t=-6（舍去）或t=1，即x2+y2=1．
    故答案是：1．

    点评 本题主要考查了换元法解一元二次方程，即把某个式子看作一个整体，用一个字母去代替它，实行等量替换．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

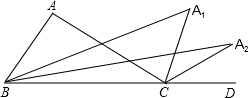    6．如图，在△ABC，∠BAC=100°，延长BC到D，∠ABC与∠ACD的角平分线相交于A1，若∠A1BC与∠A1CD的角平分线相交于点A2，以此类推，∠An-1BC与∠An-1CD的角平分线相交于点An，则∠An=$\frac{100°}{{2}^{n}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

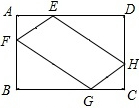    7．如图，在矩形ABCD中，AB=5，BC=6，点E，F，G，H分别在已知矩形的四条边上，且四边形EFGH也是矩形，GF=2EF．若设AE=a，AF=b，则a与b满足的关系为（　　）
    A．$\left\{\begin{array}{l}{a+b=5}\\{a+2b=6}\end{array}\right.$B．$\left\{\begin{array}{l}{a=2b}\\{2a+b=6}\end{array}\right.$C．$\left\{\begin{array}{l}{2a+b=5}\\{a+2b=6}\end{array}\right.$D．$\left\{\begin{array}{l}{2a+b=6}\\{a+2b=5}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．用配方法解下列方程时，配方正确的是（　　）
    A．方程x2-6x-5=0，可化为（x-3）2=4
    B．方程y2-2y-2015=0，可化为（y-1）2=2015
    C．方程a2+8a+9=0，可化为（a+4）2=25
    D．方程2x2-6x-7=0，可化为${（{x-\frac{3}{2}}）^2}=\frac{23}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．某商店四月份的利润为6.3万元，此后两个月进入淡季，利润均以相同的百分比下降，至六月份利润为5.4万元．设下降的百分比为x，由题意列出方程正确的是（　　）
    A．5.4（1+x）2=6.3B．5.4（1-x）2=6.3C．6.3（1+x）2=5.4D．6.3（1-x）2=5.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．已知数据x1，x2，…，xn的平均数是2，方差是3，则一组新数据x1+8，x2+8，…，xn+8的平均数和方差分别是（　　）
    A．10，3B．10，11C．2，3D．2，11

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）计算：（-3）0-$\sqrt{27}$+|1-$\sqrt{2}$|+$\frac{1}{\sqrt{3}+\sqrt{2}}$
    （2）如图：其中矩形CDEF表示楼体，AB=130米，CD=10米，∠A=30°，∠B=45°，（A、C、D、B四点在同一直线上）问：楼高多少米？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：9$\sqrt{2}×\sqrt{5}-{（{π-4}）^0}+\sqrt{{{（{3-\sqrt{10}}）}^2}}-{（{\sqrt{10}}）^3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在一个直角三角形中，斜边上的中线为4cm，则斜边长为8cm．

    查看答案和解析>>

    同步练习册答案