Question

8．如图，抛物线$y=\frac{4}{3}{x^2}+\frac{8}{3}x-4$与x轴交于A，B两点（点A在点B的左侧），与y交于点C，∠BAC的平分线与y轴交于点D，与抛物线相交于点Q，P是线段AB上一点，过点P作x轴的垂线，分别交AD，AC于点E，F，连接BE，BF．
（1）如图1，求线段AC所在直线的解析式；
（2）如图1，求△BEF面积的最大值和此时点P的坐标；
（3）如图2，以EF为边，在它的右侧作正方形EFGH，点P在线段AB上运动时正方形EFGH也随之运动和变化，当正方形EFGH的顶点G或顶点H在线段BC上时，求正方形EFGH的边长．

Answer 1

分析 （1）由抛物线解析式求得点A、C的坐标，然后根据待定系数法来求直线AC的直线方程即可；
（2）如答图2，在直角三角形AOC中利用勾股定理求得AC的长度；过点D作DI⊥AC于点I，构建全等三角形△ADI≌△ADO（SSA）和Rt△CDI，利用全等三角形的性质可以设DI=DO=m，则DC=OC-OD=4-m．所以根据勾股定理列出关于m的方程，借助于方程解题即可求得点D的坐标；然后利用待定系数法求得直线AD方程，由直线上点的坐标特征、三角形的面积公式和二次函数最值的求法来求△BEF面积的最大值和此时点P的坐标；
（3）需要分类讨论：①当顶点G在线段BC上时，如答图3．设P（t，0），则由一次函数图象上点的坐标特征和正方形的性质推知$E（{t，-\frac{1}{2}t-\frac{3}{2}}）$，$F（{t，-\frac{4}{3}t-4}）$，$G（{-\frac{1}{3}t，-\frac{4}{3}t-4}）$．所以由正方形的邻边相等得到：$\frac{5}{6}t+\frac{5}{2}=-\frac{4}{3}t$，易得EF、FG的长度，从而求得点P的坐标和正方形的边长；
同理，②当顶点H在线段BC上时，$P（{-\frac{45}{47}，0}）$，正方形的边长为$\frac{80}{47}$．

解答 解：（1）如答图1，抛物线的解析式为：$y=\frac{4}{3}{x^2}+\frac{8}{3}x-4$．
令x=0，则y=-4，
∴C（0，-4）．
令y=0，则$\frac{4}{3}{x^2}+\frac{8}{3}x-4=0$，
解得，x₁=-3，x₂=1．
∴A（-3，0），B（1，0）．
设直线AC所在直线解析式为：y=kx+b（k≠0），
将A（-3，0），C（0，-4）代入可得，$\left\{\begin{array}{l}-3k+b=0\\ b=-4\end{array}\right.$，
解得$\left\{\begin{array}{l}k=-\frac{4}{3}\\ b=-4\end{array}\right.$，
直线AC所在直线解析式为：$y=-\frac{4}{3}x-4$；

（2）过点D作DI⊥AC于点I，如答图2．
∵A（-3，0），C（0，-4），
∴OA=3．
∴OC=4．
在Rt△AOC中，$AC=\sqrt{O{A^2}+O{C^2}}=\sqrt{{3^2}+{4^2}}=5$．
∵在△ADI与△ADO中，$\left\{\begin{array}{l}{∠DIA=∠DOA=90°}\\{∠DAI=∠DAO}\\{DA=DA}\end{array}\right.$，
∴△ADI≌△ADO（SSA），
∴AI=AO=3，DI=DO．
设DI=DO=m，则DC=OC-OD=4-m．
∵IC=AC-AI，
∴IC=5-3=2．
在Rt△CDI中，∵ID²+IC²=DC²，
∴m²+2²=（4-m）²，
解得，$m=\frac{3}{2}$．
∴$OD=\frac{3}{2}$．
∴$D（{0，-\frac{3}{2}}）$．
设直线AD所在直线解析式为：y=kx+b（k≠0），
将A（-3，0），$D（{0，-\frac{3}{2}}）$代入可得，$\left\{\begin{array}{l}-3k+b=0\\ b=-\frac{3}{2}.\end{array}\right.$，
解得$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=-\frac{3}{2}.\end{array}\right.$，
直线AD所在直线解析式为：$y=-\frac{1}{2}x-\frac{3}{2}$．
又∵直线AC的解析式为：$y=-\frac{4}{3}x-4$．
∴设P（n，0），则$E（{n，-\frac{1}{2}n-\frac{3}{2}}）$，$F（{n，-\frac{4}{3}n-4}）$，
∴BP=1-n，$EF=（{-\frac{1}{2}n-\frac{3}{2}}）-（{-\frac{4}{3}n-4}）=\frac{5}{6}n+\frac{5}{2}$，
∴${S_{△BEF}}=\frac{1}{2}EF•BP=\frac{1}{2}（{\frac{5}{6}n+\frac{5}{2}}）（{1-n}）$=$-\frac{5}{12}{n^2}-\frac{5}{6}n+\frac{5}{4}（{-3≤n≤1}）$
∴该函数的对称轴是直线x=-1．
∴当x=-1时，S_△BEF的最大值=$\frac{5}{3}$．
此时，P（-1，0）；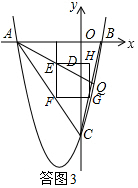

（3）由B（1，0），C（0，-4）可得直线BC的解析式为：y=4x-4．
①当顶点G在线段BC上时，如答图3．
设P（t，0），则$E（{t，-\frac{1}{2}t-\frac{3}{2}}）$，$F（{t，-\frac{4}{3}t-4}）$，$G（{-\frac{1}{3}t，-\frac{4}{3}t-4}）$．
∴$EF=（{-\frac{1}{2}t-\frac{3}{2}}）-（{-\frac{4}{3}t-4}）=\frac{5}{6}t+\frac{5}{2}$，$FG=-\frac{1}{3}t-t=-\frac{4}{3}t$．
∵EF=FG，
∴$\frac{5}{6}t+\frac{5}{2}=-\frac{4}{3}t$，
解得，$t=-\frac{15}{13}$．
∴$FG=-\frac{4}{3}×（{-\frac{15}{13}}）=\frac{20}{13}$．
∴顶点G在线段BC上时，$P（{-\frac{15}{13}，0}）$，正方形的边长为$\frac{20}{13}$；
②当顶点H在线段BC上时，如答图4．
设P（t，0），则$E（{t，-\frac{1}{2}t-\frac{3}{2}}）$，$F（{t，-\frac{4}{3}t-4}）$，$H（{-\frac{1}{8}t+\frac{5}{8}，-\frac{1}{2}t-\frac{3}{2}}）$
∴$EF=（{-\frac{1}{2}t-\frac{3}{2}}）-（{-\frac{4}{3}t-4}）=\frac{5}{6}t+\frac{5}{2}$，$EH=（{-\frac{1}{8}t+\frac{5}{8}}）-t=-\frac{9}{8}t+\frac{5}{8}$．
∵EF=EH，
∴$\frac{5}{6}t+\frac{5}{2}=-\frac{9}{8}t+\frac{5}{8}$，
解得，$t=-\frac{45}{47}$．
∴$EF=\frac{5}{6}×（{-\frac{45}{47}}）+\frac{5}{2}=\frac{80}{47}$．
∴顶点H在线段BC上时，$P（{-\frac{45}{47}，0}）$，正方形的边长为$\frac{80}{47}$．
综上所述，顶点G在线段BC上时，$P（{-\frac{15}{13}，0}）$，正方形的边长为$\frac{20}{13}$；顶点H在线段BC上时，$P（{-\frac{45}{47}，0}）$，正方形的边长为$\frac{80}{47}$．

点评 本题考查了二次函数综合题，其中涉及到了待定系数法求一次函数解析式，函数图象上点的坐标特征，二次函数最值的求法，勾股定理以及正方形的性质，此题难度较大，对于有关于动点问题的解答时，切记要分类讨论，以防漏解或错解．