
 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.分析 (1)分两种情况:m=0或m≠0分类探讨得出答案即可;
(2)首先由二次函数y=mx2-(3m-1)x+2m-2的图象经过坐标原点,求得m的数值,得出抛物线的解析式,进一步利用待定系数法求函数解析式即可;
(3)过点C作CE⊥x轴交AB于E得出∠DEC=∠OAB=45°,设出C、E坐标,表示出CE,建立二次函数求得最大值即可.
解答 (1)证明:当m=0时,x=2;
当m≠0时,△=(3m-1)2-4m(2m-2)=9m2-6m+1-8m2+8m=m2+2m+1=(m+1)2,
∵(m+1)2≥0,
∴△≥0
综上所述:无论m取任何实数时,方程恒有实数根;
(2)∵二次函数y=mx2-(3m-1)x+2m-2的图象经过坐标原点,
∴2m-2=0,
∴m=1,
抛物线C1的解析式为:y=x2-2x,
抛物线C2的解析式为:y=x2-2x-2,
设直线l所在函数解析式为:y=kx+b,
将A(0,-2)和点B(2,0)代入y=kx+b,
∴直线l所在函数解析式为:y=x-2;
(3)据题意:过点C作CE⊥x轴交AB于E,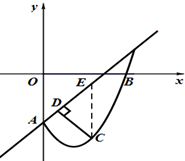
可证∠DEC=∠OAB=45°,则$CD=\frac{{\sqrt{2}EC}}{2}$,
设C(t,t2-2t-2),E(t,t-2),(0<t<3)
∴EC=yE-yC=-t2+3t=$-{({t-\frac{3}{2}})^2}+\frac{9}{4}$,
∴当$t=\frac{3}{2}$时,$E{C_{max}}=\frac{9}{4}$
∵CD随EC增大而增大,
∴$C{D_{max}}=\frac{9}{8}\sqrt{2}$为所求.
点评 此题考查抛物线与x轴交点个数与其判别式的关系,待定系数法求函数解析式,以及抛物线平移与最值问题.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
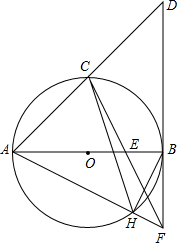 如图,AB是⊙O的直径,点C是$\widehat{AB}$的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,点C是$\widehat{AB}$的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
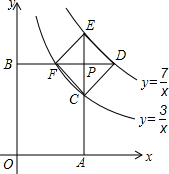 如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.
如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
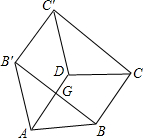 如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.
如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
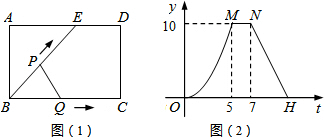
| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com