
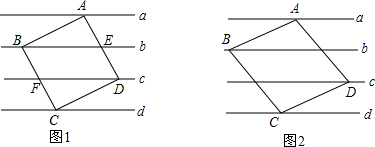
分析 (1)如图1,过B,D分别作直线d的垂线,垂足分别为P,Q,通过证得△CBP≌△CDQ,得出CP=DQ=1,然后根据勾股定理即可求得;
(2)如图2,过B,D分别作直线d的垂线,垂足分别为M,N,作∠BPC=∠DQC=120°,P,Q在直线d上,通过证得△BPC≌△DQC证得PC=DQ,通过解直角三角形求得PM,DQ,进而求得MC,然后根据勾股定理即可求得.
解答 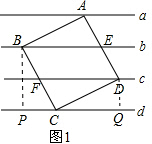 解:(1)如图1,过B,D分别作直线d的垂线,垂足分别为P,Q,
解:(1)如图1,过B,D分别作直线d的垂线,垂足分别为P,Q,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BCD=90°,
∴∠PCB+∠QCD=90°,
∵∠PBC+∠PCB=90°,
∴∠PBC=∠QCD,
在△CBP和△CDQ中
$\left\{\begin{array}{l}{∠PBC=∠QCD}\\{∠BPC=∠CQD=90°}\\{BC=CD}\end{array}\right.$
∴△CBP≌△CDQ(AAS),
∴CP=DQ=1,
∵BP=3,
∴$CB=\sqrt{{1^2}+{3^2}}=\sqrt{10}$;
(2)如图2,过B,D分别作直线d的垂线,垂足分别为M,N,作∠BPC=∠DQC=120°,P,Q在直线d上,
∵∠DCB=120°,
∴∠PCB+∠DCQ=60°,
∵∠PBC+∠PCB=60°,
∴∠PBC=∠DCQ,
在△BPC和△CQD中
$\left\{\begin{array}{l}{∠PBC=∠DCQ}\\{∠BPC=∠DQC}\\{BC=CD}\end{array}\right.$
∴△BPC≌△DQC,
∴PC=DQ,PB=CQ,
∵∠BPC=∠DQC=120°,
∴∠BPM=∠DQN=60°,
∴sin∠BPM=$\frac{BM}{PB}$,sin∠DQN=$\frac{DN}{DQ}$,
∵BM=3,DN=1,
∴PB=2$\sqrt{3}$,DQ=$\frac{2}{3}$$\sqrt{3}$,
∴PC=DQ=$\frac{2}{3}$$\sqrt{3}$,
∵∠BPM=60°,
∴∠PBM=30°,
∵在RT△PBM中,PM=$\frac{1}{2}$PB=$\sqrt{3}$,
∴MC=PC+PM=$\frac{5}{3}$$\sqrt{3}$,
∴在RT△PBM中,BC=$\sqrt{B{M}^{2}+M{C}^{2}}$=$\sqrt{{3}^{2}+(\frac{5\sqrt{3}}{3})^{2}}$=$\frac{2}{3}$$\sqrt{39}$.
点评 本题考查了正方形的性质、平行线的性质、全等三角形的判定和性质、勾股定理、解直角三角形等知识,作出辅助线构建全等三角形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )| A. | π-1 | B. | 2π-1 | C. | $\frac{1}{2}$π-1 | D. | $\frac{1}{2}$π-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
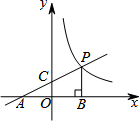 如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.
如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程 | 甲类收费(元) | 乙类收费(元) |
| 3千米以下(包含3千米) | 5.00 | 6.00 |
| 3千米以上,每增加1千米 | 1.60 | 1.30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | $\frac{24}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com