
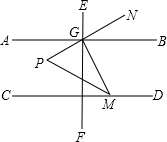
 已知,如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.
已知,如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.分析 (1)首先根据∠CMG=60°,MP平分∠GMC,可得∠PMG=30°,然后根据∠MGN=75°,应用三角形的外角的性质,求出∠MPN的度数即可.
(2)首先根据∠MGF=30°,求出∠EGM=150°,再根据PN平分∠EGM,求出∠MGN的度数;然后根据∠CMG=60°,MP平分∠GMC,求出∠PMG的度数;最后应用三角形的外角的性质,求出∠MPN的度数即可.
(3)当点M在直线CD上移动时,∠MPN的大小不变,都是45°,理由如下:设∠MGF=x°,则∠CMG=90-x°,分别求出∠MGN、∠PMG的度数,然后根据三角形的外角的性质,可得∠MGN=∠MPN+∠PMG,据此求出∠MPN的度数即可.
解答 解:(1)∵∠CMG=60°,MP平分∠GMC,
∴∠PMG=60°÷2=30°,
∵∠MGN=75°,∠MGN=∠MPN+∠PMG,
∴∠MPN=75°-30°=45°.
(2)∵∠MGF=30°,
∴∠EGM=180°-30°=150°,
∵PN平分∠EGM,
∴∠MGN=150°÷2=75°,
∵∠CMG=60°,MP平分∠GMC,
∴∠PMG=60°÷2=30°,
∵∠MGN=75°,∠MGN=∠MPN+∠PMG,
∴∠MPN=75°-30°=45°.
(3)当点M在直线CD上移动时,∠MPN的大小不变,都是45°,理由如下:
设∠MGF=x°,则∠CMG=90-x°,
∵∠MGF=x°,
∴∠EGM=180°-x°,
∵PN平分∠EGM,
∴∠MGN=(180°-x°)÷2=90°-0.5x°,
∵∠CMG=90°-x°,MP平分∠GMC,
∴∠PMG=(90°-x°)÷2=45°-0.5x°,
∵∠MGN=90°-0.5x°,∠MGN=∠MPN+∠PMG,
∴∠MPN=90°-0.5x°-(45°-0.5x°)=45°.
点评 (1)此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
(2)此题还考查了三角形的外角的性质和角平分线的性质和应用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
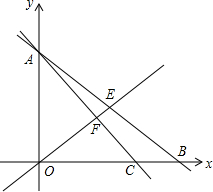 已知,如图,在y轴上有一点A(0,6),在x轴上有两点B(6,0)、C(5,0).
已知,如图,在y轴上有一点A(0,6),在x轴上有两点B(6,0)、C(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,3cm,5cm | B. | 3cm,4cm,6cm | C. | 5cm,6cm,11cm | D. | 8cm,5cm,2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对剡溪水质情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班50名同学体重情况的调查 | |
| D. | 对某品牌日光灯质量情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com