
 如图,⊙O与△ABC的三边分别相切于D、E、F,则△DEF一定是( )三角形.
如图,⊙O与△ABC的三边分别相切于D、E、F,则△DEF一定是( )三角形.| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 等腰 |
分析 连接OD,OE,OF,根据切线的性质得到∠ADO=∠AFO=90°,根据三角形的内角和得到∠A+∠DOF=180°,推出∠DEF是锐角,同理∠EDF,∠DFE是锐角,于是得到结论
解答 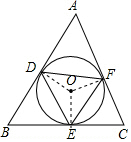 解:连接OD,OE,OF,
解:连接OD,OE,OF,
∵⊙O与△ABC的三边分别相切于D、E、F,
∴∠ADO=∠AFO=90°,
∴∠A+∠DOF=180°,
∴∠DOF=180°-∠A,
∴∠DEF=$\frac{1}{2}∠$DOF=90°-$\frac{1}{2}∠$A,
∴∠DEF是锐角,
同理∠EDF,∠DFE是锐角,
∴△DEF一定是锐角三角形,
故选A.
点评 本题考查了切线的性质,三角形的内切圆的性质,正确的作出辅助线是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
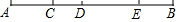 如图线段AB=9,C、D、E分别为线段AB(端点A、B除外)上顺次三个不同的点,图中所有的线段和等于46,则下列结论一定成立的是( )
如图线段AB=9,C、D、E分别为线段AB(端点A、B除外)上顺次三个不同的点,图中所有的线段和等于46,则下列结论一定成立的是( )| A. | CD=3 | B. | DE=2 | C. | CE=5 | D. | EB=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一个棱长为6的正方体盒子,一只蚂蚁从棱CD上的中点A出发,沿盒的表面爬到棱DE上后,接着又沿盒子的表面爬到盒底的B处,那么,整个爬行中,蚂蚁要爬行的最短路程为15.
如图是一个棱长为6的正方体盒子,一只蚂蚁从棱CD上的中点A出发,沿盒的表面爬到棱DE上后,接着又沿盒子的表面爬到盒底的B处,那么,整个爬行中,蚂蚁要爬行的最短路程为15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.15×l08 | B. | 1.5×106 | C. | 1.5×107 | D. | 15×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com