Question

20．已知抛物线y=$\frac{1}{5}$x²+$\frac{2}{5}$mx+$\frac{1}{5}$m²+m+3的顶点A在一条直线l上运动．
（1）A点坐标（-m，m+3），，直线l的解析式是y=-x+3．
（2）抛物线与直线l的另一个交点为B，当△AOB是直角三角形时，求m 的值．
（3）抛物线上是否存在点C使△ABC的面积是△ABO面积的2.4倍，若存在请求出C点坐标（用含m的式子表示），若不存在，请说明理由．

Answer 1

分析 （1）利用配方法求顶点A的坐标为：（-m，m+3），因为顶点A在一条直线l上运动，所以直线l的解析式是：y=-x+3；
（2）当△AOB是直角三角形时，分三种情况讨论：令三个顶点分别为直角顶点时，作垂线构建矩形AMNH，利用勾股定理或相似可以求出对应m的值；
（3）因为△ABC和△ABO有一个共同的底边AB，根据△ABC的面积是△ABO面积的2.4倍，可知对应的高是2.4倍，所以作PC∥l，得$\frac{OG}{GH}=\frac{OE}{EP}$=$\frac{1}{2.4}$，可求得P（0，10.2），得出直线PC的解析式，所以该直线与抛物线的交点就是两解析式组成的方程组的解．

解答 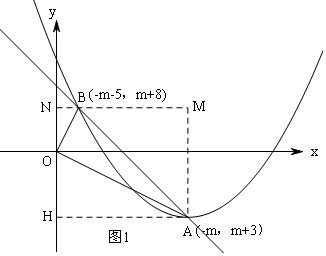解：（1）y=$\frac{1}{5}$x²+$\frac{2}{5}$mx+$\frac{1}{5}$m²+m+3，
=$\frac{1}{5}$（x+m）²+m+3，
∴顶点A（-m，m+3），
设A（x，y），则x=-m，y=m+3，
∴m=-x，y=-x+3，
∴直线l的解析式是：y=-x+3；
故答案为：（-m，m+3），y=-x+3；
（2）由题意得：$\left\{\begin{array}{l}{y=-x+3}\\{y=\frac{1}{5}{x}^{2}+\frac{2}{5}mx+\frac{1}{5}{m}^{2}+m+3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{x}_{1}=-m}\\{{y}_{1}=m+3}\end{array}\right.$   $\left\{\begin{array}{l}{{x}_{2}=-m-5}\\{{y}_{2}=m+8}\end{array}\right.$，
∵A（-m，m+3），
∴B（-m-5，m+8），
作AH⊥y轴于H，作BN⊥y轴于N，作AM⊥BN于M，
则OA²=AH²+OH²=（-m）²+（m+3）²=2m²+6m+9，
OB²=BN²+ON²=（-m-5）²+（m+8）²=2m²+26m+89，
AB²=BM²+AM²=[-m-（-m-5）]²+（m+8-m-3）²=50，
∴BN=-m-5，BM=-m-（-m-5）=5，AM=m+8-m-3=5，OH=-m-3，ON=m+8，
分情况讨论：
①当∠AOB=90°时，如图1，
方法一：
∴∠NOB+∠AOH=90°，
∵∠AOH+∠OAH=90°，
∴∠NOB=∠OAH，
∵∠ONB=∠AHO=90°，
∴△BNO∽△OHA，
∴$\frac{BN}{OH}=\frac{ON}{AH}$，
∴$\frac{-m-5}{-m-3}=\frac{m+8}{-m}$，
∴m²+8m+12=0，
（m+2）（m+6）=0，
m₁=-2，m₂=-6，
方法二：则OB²+OA²=AB²，
∴m²+8m+12=0，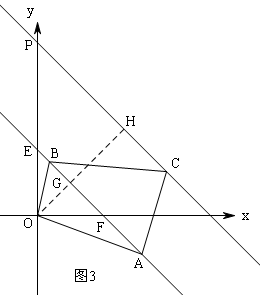
（m+2）（m+6）=0，
m₁=-2，m₂=-6，
②当∠ABO=90°时，如图2，
方法一：
同理得：△BNO∽△AMB，
∴$\frac{BN}{AM}=\frac{ON}{BM}$，
∴$\frac{-m-5}{5}$=$\frac{m+8}{5}$，
m=-$\frac{13}{2}$，
方法二：则OB²+AB²=OA²，
∴20m+130=0，
m=-$\frac{13}{2}$，
③当∠OAB=90°时，OA²+AB²=OB²，
2m²+6m+9+50=2m²+26m+89，
20m=-30，
m=-$\frac{3}{2}$，
综上所述，m的值为-2或-6或-$\frac{13}{2}$或-$\frac{3}{2}$；
（3）如图3，过C作CP∥l，交y轴于P，过O作OH⊥PC于H，交l于G，则OH⊥l，
设直线l与两坐标轴交于E、F，
当x=0时，y=3，
当y=0时，x=3，
∴OE=OF=3，
∵S_△ABC=2.4S_△ABO，
∴$\frac{OG}{GH}$=$\frac{1}{2.4}$，
∵EF∥PC，
∴$\frac{OG}{GH}=\frac{OE}{EP}$=$\frac{1}{2.4}$，
∴$\frac{3}{EP}=\frac{1}{2.4}$，
∴EP=7.2，
∴P（0，10.2），
则直线PC的解析式为：y=-x+10.2，
∴$\left\{\begin{array}{l}{y=-x+10.2}\\{y=\frac{1}{5}{x}^{2}+\frac{2}{5}mx+\frac{1}{5}{m}^{2}+m+3}\end{array}\right.$，
$\frac{1}{5}{x}^{2}+\frac{2}{5}mx+\frac{1}{5}{m}^{2}+m+3$=-x+10.2，
x²+2mx+m²+5m+15+5x-51=0，
x²+（2m+5）x+m²+5m-36=0，
（x+m+9）（x+m-4）=0，
x₁=-m-9，x₂=-m+4，
当x₁=-m-9时，y₁=m+19.2，
当x₂=-m+4时，y₂=m+6.2，
∴C（-m-9，m+19.2）或（-m+4，m+6.2）．
当直线PC∥l，且PC在l的下方时，
同理得EP=7.2，
∴P（0，-4.2），
∴直线PC的解析式为：y=-x-4.2，
则$\left\{\begin{array}{l}{y=-x-4.2}\\{y=\frac{1}{5}{x}^{2}+\frac{2}{5}mx+\frac{1}{5}{m}^{2}+m+3}\end{array}\right.$，
此方程组无解，
综上所述，点C的坐标为（-m-9，m+19.2）或（-m+4，m+6.2）．

点评 本题是二次函数的综合题，考查了二次函数的性质、三角形的面积、勾股定理、相似三角形的性质和判定等知识，熟练掌握两函数的交点就是两解析式组成的方程组的解，对于给出的直角三角形时，要采用分类讨论的方式解决问题．