
 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.分析 (1)求出△ACD≌△AED,根据全等三角形的性质得出即可;
(2)求出AD=BD,推出∠B=∠DAB=∠CAD,求出∠B=30°,即可求出BD=2CD=8,根据勾股定理求出即可.
解答 (1)证明:∵在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,
∴CD=DE,∠AED=∠C=90°,∠CAD=∠EAD,
在△ACD和△AED中
$\left\{\begin{array}{l}{∠CAD=∠EAD}\\{∠C=∠AED}\\{AD=AD}\end{array}\right.$
∴△ACD≌△AED,
∴AC=AE;
(2)解:∵DE⊥AB,点E为AB的中点,
∴AD=BD,
∴∠B=∠DAB=∠CAD,
∵∠C=90°,
∴3∠B=90°,
∴∠B=30°,
∵CD=DE=4,∠DEB=90°,
∴BD=2DE=8,
由勾股定理得:BE=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$.
点评 本题考查了角平分线性质,全等三角形的性质和判定,含30度角的直角三角形性质,勾股定理,三角形内角和定理,线段垂直平分线性质,等腰三角形的性质的应用,能推出△ACD≌△AED和求出∠B=30°是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5,12,13 | B. | 9,12,15 | C. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | D. | 0.3,0.4,0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
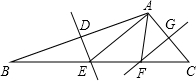 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点G、F,若∠BAC=115°,则∠EAF=50°.
如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点G、F,若∠BAC=115°,则∠EAF=50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
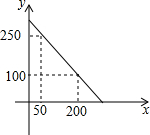 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com