
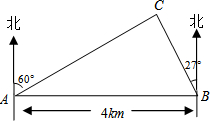
 如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).
如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).分析 如图,过点C作CD⊥AB,构建直角△ACD和直角△BCD.通过解Rt△BDC得到BD=0.5CD.通过解Rt△ADC得到AD=$\sqrt{3}$CD,所以由AB=4km科研求得CD的长度.最后通过解Rt△ADC来求AC的长度.
解答 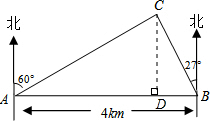 解:如图,过点C作CD⊥AB,则∠BCD=27°,∠ACD=60°,
解:如图,过点C作CD⊥AB,则∠BCD=27°,∠ACD=60°,
在Rt△BDC中,由tan∠BCD=$\frac{BD}{CD}$,
∴BD=CD tan27°=0.5CD.
在Rt△ADC中,由tan∠ACD=$\frac{AD}{CD}$
∴AD=CD•tan60°=$\sqrt{3}$CD.
∵AD+BD=$\sqrt{3}$CD+0.5CD=4,
∴CD=$\frac{4}{\sqrt{3}+0.5}$.
在Rt△ADC中,∵∠ACD=60°,
∴∠CAD=30°,
∴AC=2CD=$\frac{8}{\sqrt{3}+0.5}$≈3.6.
∴灯塔C与观测点A的距离为3.6km.
点评 此题主要考查了解直角三角形-方向角问题的应用,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


科目:初中数学 来源: 题型:选择题
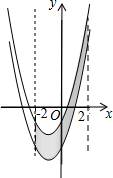 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )| A. |  | B. | 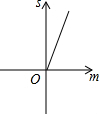 | C. | 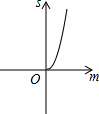 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
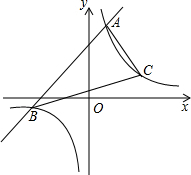 已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
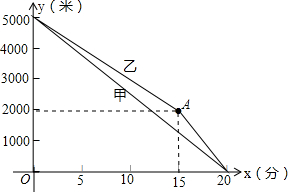 甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
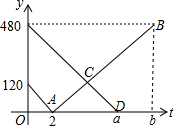 甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的$\frac{3}{4}$,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.
甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的$\frac{3}{4}$,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com