
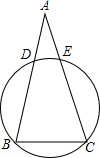
 如图,$\widehat{BD}$=$\widehat{CE}$,求证:AB=AC.
如图,$\widehat{BD}$=$\widehat{CE}$,求证:AB=AC. 分析 先由$\widehat{BD}$=$\widehat{CE}$得到$\widehat{BE}$=$\widehat{CD}$,则根据圆心角、弧、弦的关系得到∠C=∠B,然后利用等腰三角形的判定即可得到AB=AC.
解答 证明:∵$\widehat{BD}$=$\widehat{CE}$,
∴$\widehat{BD}$+$\widehat{DE}$=$\widehat{CE}$+$\widehat{DE}$,
即$\widehat{BE}$=$\widehat{CD}$,
∴∠C=∠B,
∴AB=AC.
点评 本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.


科目:初中数学 来源: 题型:解答题
 如图,将一张正方形铁片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体容器,设这个正方形铁片的边长为a,做成的无盖长方体容器高为h.
如图,将一张正方形铁片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体容器,设这个正方形铁片的边长为a,做成的无盖长方体容器高为h.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如果所示,已知∠1=∠2,∠3=∠4,则下列结论正确的个数为( )
如果所示,已知∠1=∠2,∠3=∠4,则下列结论正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com