
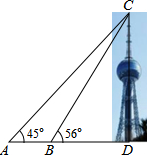
 某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为189m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)
某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为189m.(sin56°≈0.83,tan56°≈1.49,结果保留整数) 分析 首先根据题意得:∠CAD=45°,∠CBD=56°,AB=62m,在Rt△ACD中,易求得BD=AD-AB=CD-62;在Rt△BCD中,可得BD=$\frac{CD}{tan56°}$,即可得AB=AD-BD=CD-$\frac{CD}{tan56°}$=62,继而求得答案.
解答 解:根据题意得:∠CAD=45°,∠CBD=56°,AB=62m,
∵在Rt△ACD中,∠ACD=∠CAD=45°,
∴AD=CD,
∵AD=AB+BD,
∴BD=AD-AB=CD-2(m),
∵在Rt△BCD中,tan∠CBD=$\frac{CD}{BD}$,
∴BD=$\frac{CD}{tan56°}$,
∴AB=AD-BD=CD-$\frac{CD}{tan56°}$=62,
∴CD≈189,(m).
答:蒲宁之珠的高度CD约为189,
故答案为:189.
点评 本题考查了仰角的知识.此题难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.


科目:初中数学 来源: 题型:填空题
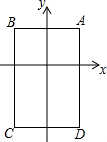 在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).
在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
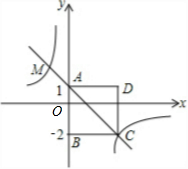 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
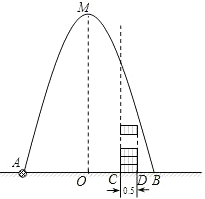 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少8个时,网球可以落入桶内.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少8个时,网球可以落入桶内.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com