
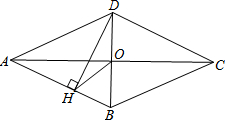
 如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=25度.
如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=25度. 分析 根据菱形的对角线互相平分可得OD=OB,再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB,然后根据等边对等角求出∠OHB=∠OBH,根据两直线平行,内错角相等求出∠OBH=∠ODC,然后根据等角的余角相等解答即可.
解答 解:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=$\frac{1}{2}$BD=OB,
∴∠OHB=∠OBH,
又∵AB∥CD,
∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO=$\frac{1}{2}∠DAB$=25°,
故答案为:25.
点评 本题考查了菱形的对角线互相垂直平分的性质,直角三角形斜边上的中线等于斜边的一半的性质,以及等角的余角相等,熟记各性质并理清图中角度的关系是解题的关键.


科目:初中数学 来源: 题型:填空题
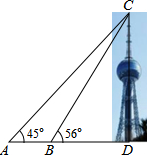 某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为189m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)
某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为189m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
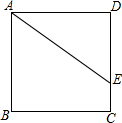 如图,E为正方形ABCD边CD上一点,DE=3,CE=1,F为直线BC上一点,直线DF与直线AE交于G,且DF=AE,则DG=$\frac{12}{5}$或$\frac{60}{7}$.
如图,E为正方形ABCD边CD上一点,DE=3,CE=1,F为直线BC上一点,直线DF与直线AE交于G,且DF=AE,则DG=$\frac{12}{5}$或$\frac{60}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线
已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线查看答案和解析>>
科目:初中数学 来源: 题型:解答题
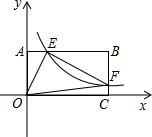 如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=$\frac{k}{x}$(x>0)的图象与边BC交与点F.
如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=$\frac{k}{x}$(x>0)的图象与边BC交与点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
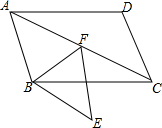 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
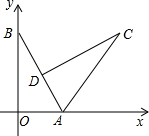 如图,平面直角坐标系中,已知O为坐标原点,A(3,0),B(0,4).将Rt△AOB绕点A顺时针旋转得到Rt△ACD,旋转后点D恰好落在AB边上时,则D点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
如图,平面直角坐标系中,已知O为坐标原点,A(3,0),B(0,4).将Rt△AOB绕点A顺时针旋转得到Rt△ACD,旋转后点D恰好落在AB边上时,则D点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(1,2) | B. | y随x的增大而减少 | ||
| C. | 图象在第一、三象限 | D. | 若x>1,则y<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com