
 如图所示,四边形OABC是矩形,点A,C的坐标分别为(3,0),(0,l),点D是线段BC上的动点(与端点B,C不重合),过点D作直线y=-$\frac{1}{2}$x+b交折线OAB于点E.
如图所示,四边形OABC是矩形,点A,C的坐标分别为(3,0),(0,l),点D是线段BC上的动点(与端点B,C不重合),过点D作直线y=-$\frac{1}{2}$x+b交折线OAB于点E.分析 (1)根据待定系数法,将A、B点坐标代入,可得答案;
(2)要表示出△ODE的面积,要分两种情况讨论,①如果点E在OA边上,只需求出这个三角形的底边OE长(E点横坐标)和高(D点纵坐标),代入三角形面积公式即可;②如果点E在AB边上,这时△ODE的面积可用长方形OABC的面积减去△OCD、△OAE、△BDE的面积;
(3)根据函数的最值在函数图象的端点,可得答案;
(4)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化
解答 解:(1))∵四边形OABC是矩形,点A、C的坐标分别为(3,0),C(0,1),
∴B(3,1).
若直线经过点A(3,0)时,则b=$\frac{3}{2}$,
若直线经过点B(3,1)时,则b=$\frac{5}{2}$.
点E在AB边上,b的取值范围是$\frac{3}{2}$≤b≤$\frac{5}{2}$;
(2)∵四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),
∴B(3,1),
若直线经过点A(3,0)时,则b=$\frac{3}{2}$
若直线经过点B(3,1)时,则b=$\frac{5}{2}$
若直线经过点C(0,1)时,则b=1
①若直线与折线OAB的交点在OA上时,即1<b≤$\frac{3}{2}$,如图1: ,
,
此时E(2b,0)
∴S=$\frac{1}{2}$OE•CO=$\frac{1}{2}$×2b×1=b;
②若直线与折线OAB的交点在BA上时,即$\frac{3}{2}$<b<$\frac{5}{2}$,如图2: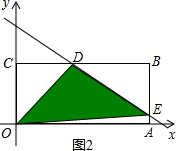 ,
,
此时E(3,b-$\frac{3}{2}$),D(2b-2,1),
∴S=S矩-(S△OCD+S△OAE+S△DBE)
=3-[$\frac{1}{2}$(2b-2)×1+$\frac{1}{2}$×3(b-$\frac{3}{2}$)+$\frac{1}{2}$×(5-2b)•($\frac{5}{2}$-b)]
=$\frac{5}{2}$b-b2,
∴S=$\left\{\begin{array}{l}{b(1<b≤\frac{3}{2})}\\{\frac{5}{2}b-{b}^{2}(\frac{3}{2}<b<\frac{5}{2})}\end{array}\right.$;
(3)当1<b≤$\frac{3}{2}$时,S最大=$\frac{3}{2}$;
当$\frac{3}{2}$<b<$\frac{5}{2}$时,S=-(b-$\frac{5}{4}$)2+$\frac{25}{16}$,
当b=$\frac{3}{2}$时,S最大=-$\frac{1}{16}$+$\frac{25}{16}$=$\frac{3}{2}$,
综上所述:当b=$\frac{3}{2}$时,S最大=-$\frac{1}{16}$+$\frac{25}{16}$=$\frac{3}{2}$;
(4)如图3: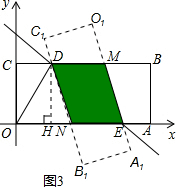 ,
,
设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积.
由题意知,DM∥NE,DN∥ME,
∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∵∠MDE=∠NED,
∴∠MED=∠MDE,
∴MD=ME,
∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,设菱形DNEM的边长为a,
由题意知,D(2b-2,1),E(2b,0),
∴DH=1,HE=2b-(2b-2)=2,
∴HN=HE-NE=2-a,
则在Rt△DHN中,由勾股定理知:a2=(2-a)2+12,
∴a=$\frac{5}{4}$,
∴S四边形DNEM=NE•DH=$\frac{5}{4}$.
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为$\frac{5}{4}$.
点评 本题考查了一次函数综合题,本题是一个动态图形中的面积是否变化的问题,看一个图形的面积是否变化,关键是看决定这个面积的几个量是否变化,本题题型新颖,是个不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度.


科目:初中数学 来源: 题型:解答题
 如图所示,抛物线y=ax2-x+c的图象经过A(-1,0)、B(0,-2)两点.
如图所示,抛物线y=ax2-x+c的图象经过A(-1,0)、B(0,-2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
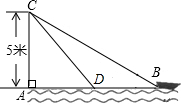 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com