
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.分析 (1)作辅助线,连接OD.根据切线的判定定理,只需证DF⊥OD即可;
(2)①连接BD.根据BE、DF两切线的性质证明△BDE∽△ABE;又由角平分线的性质、等腰三角形的两个底角相等求得△ABE∽△AFD,所以△BDE∽△AFD;最后由相似三角形的对应边成比例求得$\frac{BE}{AD}$=$\frac{DE}{DF}$=$\frac{2}{3}$;②连接OC,交AD于G,由①,设BE=2x,则AD=3x,由于△BDE∽△ABE,得到比例式求得AD=3x=6,BE=2x=4,AE=AD+DE=8,根据特殊角的三角函数值即可得到结果.
解答 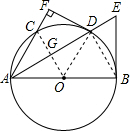 (1)证明:如图,连结OD,
(1)证明:如图,连结OD,
∵AD平分∠BAC,
∴∠DAF=∠DAO,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠DAF=∠ODA,
∴AF∥OD,
∵DF⊥AC,∴OD⊥DF,
∴DF是⊙O的切线,
(2)解:①连接BD,
∵直径AB,
∴∠ADB=90°,
∵圆O与BE相切,
∴∠ABE=90°,
∵∠DAB+∠DBA=∠DBA+∠DBE=90°,
∴∠DAB=∠DBE,
∴∠DBE=∠FAD,
∵∠BDE=∠AFD=90°,
∴△BDE∽△AFD,
∴$\frac{BE}{AD}$=$\frac{DE}{DF}$=$\frac{2}{3}$;
②连接OC,交AD于G,
由①,设BE=2x,则AD=3x,
∵△BDE∽△ABE,∴$\frac{BE}{AE}=\frac{DE}{BE}$,∴$\frac{2x}{3x+2}=\frac{2}{2x}$,
解得:x1=2,x2=-$\frac{1}{2}$(不合题意,舍去),
∴AD=3x=6,BE=2x=4,AE=AD+DE=8,
∴sin∠EAB=$\frac{1}{2}$,
∴∠EAB=30°,
∴∠FAB=60°.
点评 本题考查了切线的性质、相似三角形的判定与性质.比较复杂,解答此题的关键是作出辅助线,利用数形结合解答.


科目:初中数学 来源: 题型:填空题
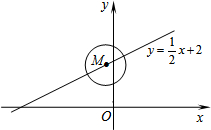 ⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
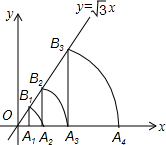 如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).
如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
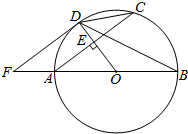 如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.
如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
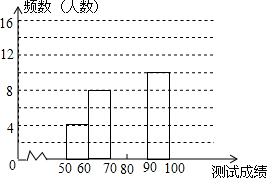 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
| 合计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
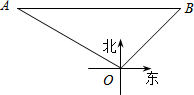 在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.
在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com