
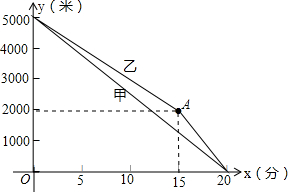
 甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:分析 (1)先根据图象信息可知,他们在进行5000米的长跑训练,再根据直线倾斜程度即可知甲的速度较快;
(2)设乙距终点的路程y(米)和跑步时间x(分)之间的函数关系式为y=kx+b,分两种情况进行讨论:①0<x<15;②15≤x≤20,根据图象上点的坐标利用待定系数法分别求出即可;
(3)由甲运动员的图象经过(0,5000),(20,0),先运用待定系数法求出甲距终点的路程y(米)和跑步时间 x(分)之间的函数关系式,再将x=15代入,得出甲距终点的路程y,又由图象可知此时乙距终点的路程,两者相减即可;
(4)先分别求出在15<x<20的时间段内,两人的速度,再将它们相减即可.
解答 解:(1)根据图象信息可知,他们在进行5000米的长跑训练,
在0<x<15的时间段内,直线y甲的倾斜程度大于直线y乙的倾斜程度,所以甲的速度较快.
故答案为5000,甲;
(2)设乙距终点的路程y(米)和跑步时间x(分)之间的函数关系式为y=kx+b.
①如果0<x<15,
将(0,5000),(15,2000)代入,
得$\left\{\begin{array}{l}{b=5000}\\{15k+b=2000}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-200}\\{b=5000}\end{array}\right.$,
所以y=-200x+5000;
②如果15≤x≤20,
将(15,2000),(20,0)代入,
得$\left\{\begin{array}{l}{15k+b=2000}\\{20k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-400}\\{b=8000}\end{array}\right.$,
所以y=-400x+8000;
综上所述,乙距终点的路程y(米)与跑步时间x(分)之间的函数关系式为:$y=\left\{{\begin{array}{l}{-200x+5000(0<x<15)}\\{-400x+8000(15≤x≤20)}\end{array}}\right.$;
(3)设甲距终点的路程y(米)和跑步时间 x(分)之间的函数关系式为:y=mx+n,
∵直线y=mx+n经过点(0,5000),(20,0),
∴$\left\{\begin{array}{l}{n=5000}\\{20m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-250}\\{n=5000}\end{array}\right.$,
∴y=-250x+5000,
∴当x=15时,甲距终点的路程y=-250×15+5000=1250,
∵由图象可知此时乙距终点的路程为2000,
∴2000-1250=750.
即当x=15时,两人相距750米;
(4)∵当15<x<20时,甲的速度为5000÷20=250,乙的速度为2000÷5=400,
又∵400-250=150,
∴在15<x<20的时间段内,两人速度之差为150米/分.
点评 此题考查了一次函数的应用,涉及的知识有:待定系数法求一次函数解析式,一次函数的性质,读懂图形中的数据是解决本题的关键.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:选择题
 如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )| A. | 4cm | B. | 5cm | C. | $\frac{15}{4}$cm | D. | $\frac{25}{4}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
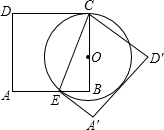 如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.
如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
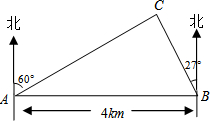 如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).
如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
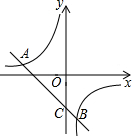 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A (-3,1),B (1,n)两点.
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A (-3,1),B (1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
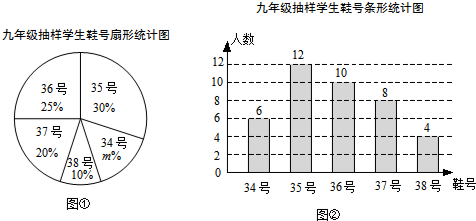
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
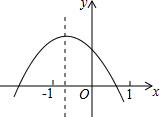 已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )| A. | a+b+c>0 | B. | b2-4ac<0 | C. | a-b+c>0 | D. | ab<0,c<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
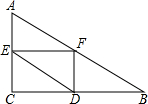 已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )
已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )| A. | 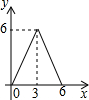 | B. | 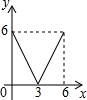 | C. | 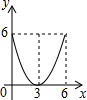 | D. | 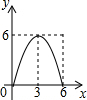 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )| A. | CE=DE | B. | AE=OE | C. | $\widehat{BC}$=$\widehat{BD}$ | D. | △OCE≌△ODE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com