
 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{16}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\sqrt{2}$-1 |
分析 连接AC1,AO,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1,进而求出DC1=OD,根据三角形的面积计算即可.
解答 方法一: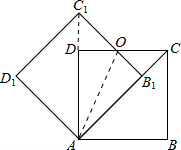 解:连接AC1,
解:连接AC1,
∵四边形AB1C1D1是正方形,
∴∠C1AB1=$\frac{1}{2}$×90°=45°=∠AC1B1,
∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,
∴∠B1AB=45°,
∴∠DAB1=90°-45°=45°,
∴AC1过D点,即A、D、C1三点共线,
∵正方形ABCD的边长是1,
∴四边形AB1C1D1的边长是1,
在Rt△C1D1A中,由勾股定理得:AC1=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
则DC1=$\sqrt{2}$-1,
∵∠AC1B1=45°,∠C1DO=90°,
∴∠C1OD=45°=∠DC1O,
∴DC1=OD=$\sqrt{2}$-1,
∴S△ADO=$\frac{1}{2}$×OD•AD=$\frac{\sqrt{2}-1}{2}$,
∴四边形AB1OD的面积是=2×$\frac{\sqrt{2}-1}{2}$=$\sqrt{2}$-1,
方法二:
解:∵四边形ABCD是正方形,
∴AC=$\sqrt{2}$,∠OCB1=45°,
∴CB1=OB1
∵AB1=1,
∴CB1=OB1=AC-AB1=$\sqrt{2}$-1,
∴S△OB1C=$\frac{1}{2}$•OB1•CB1=$\frac{1}{2}$($\sqrt{2}$-1)2,
∵S△ADC=$\frac{1}{2}$AD•AC=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
∴S四边形AB1OD=S△ADC-S△OB1C=$\frac{1}{2}$-$\frac{1}{2}$($\sqrt{2}$-1)2=$\sqrt{2}$-1;
故选:D.
点评 本题考查了正方形性质,勾股定理等知识点,主要考查学生运用性质进行计算的能力,正确的作出辅助线是解题的关键.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
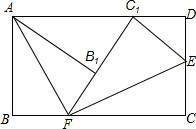 已知四边形ABCD是矩形,BF=1,FC=3,沿EF,AF折叠,点C落在C1处,点B落在FC1边上的B1,求AB=$\sqrt{5}$.
已知四边形ABCD是矩形,BF=1,FC=3,沿EF,AF折叠,点C落在C1处,点B落在FC1边上的B1,求AB=$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A、B、C都是数轴上的点,点B、C到点A的距离相等,若点A、B表示的数分别是2,$\sqrt{19}$,则点C表示的数为( )
如图,点A、B、C都是数轴上的点,点B、C到点A的距离相等,若点A、B表示的数分别是2,$\sqrt{19}$,则点C表示的数为( )| A. | 2-$\sqrt{19}$ | B. | $\sqrt{19}$-2 | C. | 4-$\sqrt{19}$ | D. | $\sqrt{19}$-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com