
 完成下面填空.
完成下面填空. 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
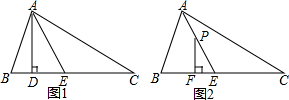
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
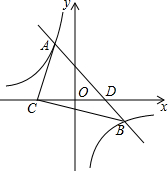 如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称.
如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
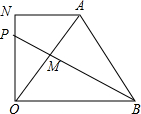 如图,在直角梯形ABON中,AN∥BO,∠ANO=90°,点A恰好在线段OB垂直平分线上,P为ON上一点,∠OPB=∠OAB,OA、OB交于点M,若ON=3,求OP+PB的值.
如图,在直角梯形ABON中,AN∥BO,∠ANO=90°,点A恰好在线段OB垂直平分线上,P为ON上一点,∠OPB=∠OAB,OA、OB交于点M,若ON=3,求OP+PB的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com