
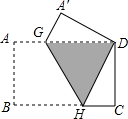
 已知矩形纸片ABCD中,AB<BC,AB=4.将它沿GH折叠,如图,使点B与点D重合.当折叠后纸片重叠部分(即图中阴影部分)的面积占矩形纸片面积的$\frac{5}{16}$时,则BC的长为8.
已知矩形纸片ABCD中,AB<BC,AB=4.将它沿GH折叠,如图,使点B与点D重合.当折叠后纸片重叠部分(即图中阴影部分)的面积占矩形纸片面积的$\frac{5}{16}$时,则BC的长为8. 分析 由折叠的性质得出A′G=AG,A′D=AB=4,∠A′=∠A=90°,设AD=BC=x,DG=y,则A′G=AG=x-y,由面积关系和勾股定理得出方程组,解方程组即可.
解答 解:由折叠的性质得:A′G=AG,A′D=AB=4,∠A′=∠A=90°,
设AD=BC=x,DG=y,则A′G=AG=x-y,
根据题意得:$\left\{\begin{array}{l}{\frac{5}{16}x×4x=\frac{1}{2}×4y}\\{{4}^{2}+(x-y)^{2}={y}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=5}\end{array}\right.$,
即BC的长为8;
故答案为:8.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理、三角形的面积关系;熟练掌握翻折变换的性质,根据面积关系和勾股定理得出方程组是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
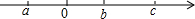 有理数a、b、c在数轴上的位置如图.
有理数a、b、c在数轴上的位置如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.383×108 | B. | 3.83×107 | C. | 38.3×106 | D. | 383×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8a2b3 | B. | 4ab3 | C. | 8a2b4 | D. | 4a2b3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com